Redes Neuronales Convoluciones con arquitectura Pytorch

Redes Neuronales Convoluciones con arquitectura Pytorch#

Introducción#

Las redes convolucionales ([LeCun et al., 1989]), también conocidas como redes neuronales convolucionales, (o convolutional neural networks CNN o ConvNet) , son un tipo especializado de red neuronal utilizadas para procesar datos con una topología en cuadrícula.

Las ConvNet se diseñaron para procesar imágenes y tratan de simular el funcionamiento de la visión humana. Restringen la arquitectura para usar un conjunto de pesos más reducido. En particular, a diferencia de una red neuronal densa, las capas ConvNet tienen neuronas dispuestas en 3 dimensiones: ancho, alto, profundidad (se adoptan las iniciales en inglés \(w,h,d\)). En las redes neuronales densas se tiene una matriz de pesos \((m,n)\) para conectar una capa anterior de \(n\) neuronas con una de \(m\). Aquí se conectarán las \(n\) neuronas con \(d\) capas convolucionales usando un bloque de \((w,h,d)\) pesos. La reducción de complejidad viene dado porque la dimensión de \((w,h)\) es muy inferior a \((m,n)\)

Una operación de convolución básica se aplica a una imagen bidimensional I, usando un kernel o filtro K bidimensional y que da como resultado una nueva imagen S:

\[S(i,j)=(K*I)(i,j)=\displaystyle\sum_{m}\displaystyle\sum_{n}=I(m,n)K(i-m,j-n)\]

Un ejemplo gráfico del proceso de convolución para una entrada con 3 canales y dimensión 5x5 \((W_1=5, H_1=5, D_1=3)\) al que se le aplica un filtro 3x3 con un salto de 2 y un relleno a cero de 1 obteniendo 2 canales de salida \((K=2, F=3, S=2, P=1)\) es

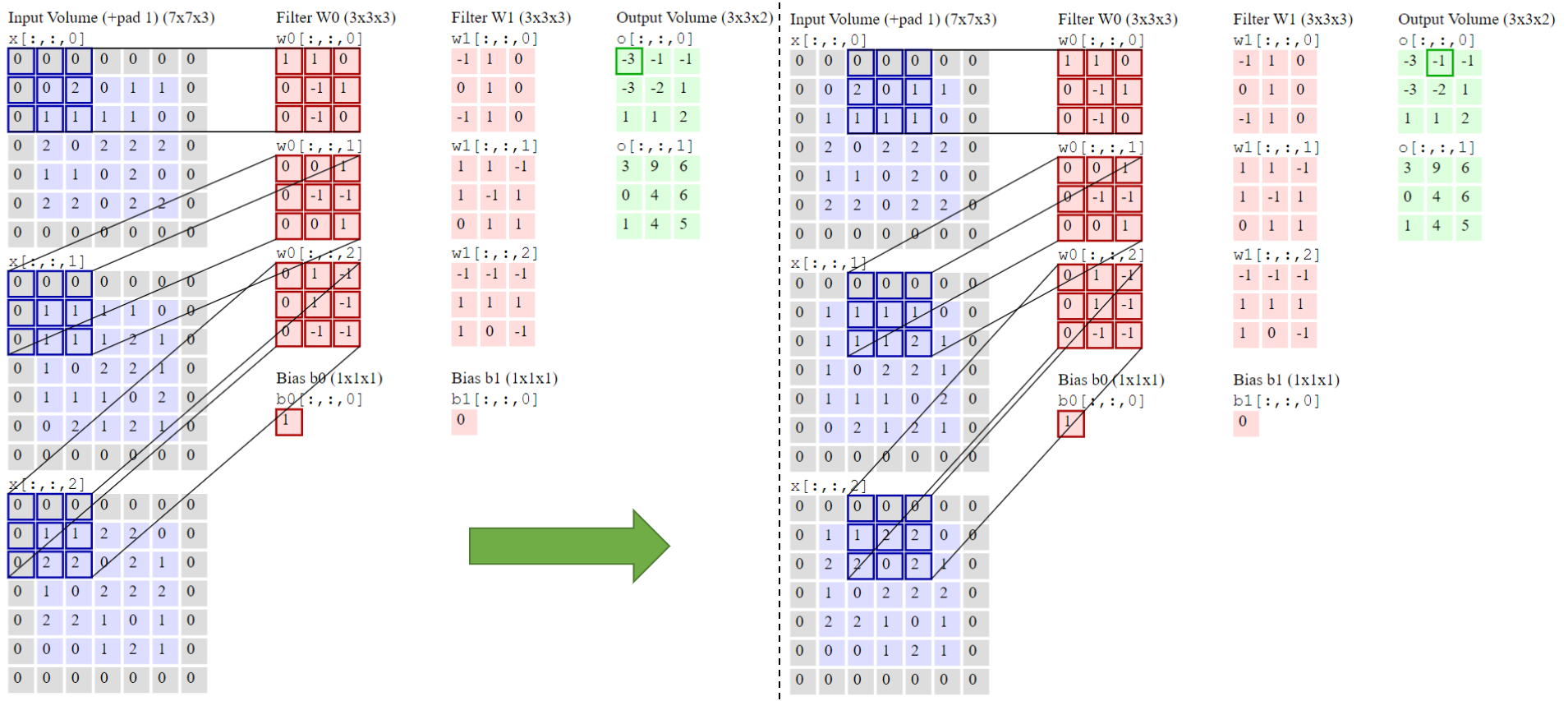
Como se puede comprobar el elemento \(-3\) del primer mapa de salida se obtiene multiplicando uno a uno los elementos de cada filtro por los canales de entrada y sumando todos los productos más el valor del bias. Idem para el siguiente elemento \(-1\) una vez ejecutado el salto hacia la derecha en columnas. Una vez llegado hasta la última columna se ejecuta un salto en filas. El relleno a ceros (padding) permite al filtro barrer todo el mapa de entrada y obtener en salida un mapa de igual dimensión. El salto (strike) en el desplazamiento provoca una reducción en la dimensión del mapa de salida.

Una Arquitectura Convolucional tipo estará compuesta por las capas: [INPUT - CONV - RELU - POOL - FC]. Cuyo detalle es:

INPUT contendrá los valores en píxeles de la imagen, en este caso una imagen de ancho b, altura h, y con tres canales de color R, G, B. El vector de datos de entrada va a ser un tensor o matriz de 4 dimensiones (n, c, b, h), donde n representará el número de observaciones en el lote tratado, c el número de canales, b es el ancho de la imagen y h es la altura de la imagen.
Los filtros que conectan los pixels localmente son compartidos y son aprendibles. Los parámetros entrenables del filtro de una capa \(l\) (\(W_l\)) tiene dimensiones (co, ci, f, f), donde co es el número de canales de salida (los canales del tensor \(Z_l\)), ci es el número de canales de entrada (los canales del tensor \(A_{l-1}\)) y f es el tamaño del filtro. Además se incluye un parámetro de bias \(B_l\), que es un vector de dimensiones (co).
La capa RELU aplicará una función de activación por elementos, como el umbral \((max(0,x))\) en cero. Esto deja el tamaño del tensor de esta capa sin cambios (n, c, b, h).
La capa POOL realizará una operación de downsampling a lo largo de las dimensiones espaciales (ancho, alto), lo que dará como resultado un volumen (n, c, b*, h*), siendo (b*,h*) inferiores a (b,h). Esta capa no utiliza pesos aprendibles.
La capa FC o densa (es decir, totalmente conectada) calculará los puntajes de clase. Las capas densas tienen una matriz entrenable \(W_l\) de dos dimensiones (m,p), siendo m el nº de carácteristicas de la salida de la capa (el vector \(X_l\)) y p el número de características de la entrada a la capa (el vector \(A_{l-1}\))

Reglas generales para modelar una red convolucional#

La capa de entrada (que contiene la imagen) debe ser divisible por \(2^n\). Los números comunes incluyen 32 (por ejemplo, CIFAR-10), 64, 96 (por ejemplo, STL-10) o 224 (por ejemplo, ImageNet), 384 y 512.

Las capas conv deben usar filtros pequeños (por ejemplo, 3x3 o como máximo 5x5), usar un salto de \(S = 1\) y, lo que es más importante, rellenar el volumen de entrada con ceros (padding) de tal manera que la capa conv no altere las dimensiones espaciales de la entrada (si F = 3, P = 1; si F = 5, P=2; en general \(P = (F - 1)/2\)).

Las capas de pool se encargan de reducir el muestreo de las dimensiones espaciales de la entrada. La configuración más común es usar max-pooling con campos receptivos 2x2 (es decir, F = 2), y un salto de 2 (S = 2); esto es, se descarta exactamente el 75%. Más infrecuente, por la dificultad de encajarlo en la dimensión de la entrada es el uso de F = 3 y S = 2. Dimensiones de maxpooling superiores son muy infrecuentes ya que es muy agresiva y deficitaria y conduce a peores rendimentos.

Algunas arquitecturas convolucionales destacadas#

Hay varias arquitecturas en el campo de las Redes Convolucionales que tienen un nombre. Los más comunes son:

LeNet. Las primeras aplicaciones exitosas de redes convolucionales fueron desarrolladas por [LeCun et al., 1998] en la década de 1990. De estos, el más conocido es la arquitectura LeNet que se utilizaba para leer códigos postales, dígitos, etc.
AlexNet. El primer trabajo que popularizó las redes convolucionales en visión artificial fue el AlexNet, desarrollado por [Krizhevsky et al., 2012] (2012). AlexNet se presentó al desafío ImageNet ILSVRC en 2012 y superó significativamente al segundo finalista (error top 5 del 16% en comparación con el subcampeón con un error del 26%). La red tenía una arquitectura muy similar a LeNet, pero era más profunda, más grande y presentaba capas convolucionales apiladas una encima de la otra (anteriormente era común tener una sola capa CONV siempre seguida inmediatamente por una capa POOL).
ZF Neto. El ganador de ILSVRC 2013 fue una Red Convolucional de Matthew Zeiler y Rob Fergus. Se hizo conocido como ZFNet (abreviatura de Zeiler & Fergus Net). Fue una mejora en AlexNet al ajustar los hiperparámetros de la arquitectura, en particular al expandir el tamaño de las capas convolucionales medias y hacer que el paso y el tamaño del filtro en la primera capa sean más pequeños.
GoogLeNet. El ganador de ILSVRC 2014 fue una red convolucional de [Szegedy et al., 2014] de Google. Su principal contribución fue el desarrollo de un Módulo de Inicio que redujo drásticamente el número de parámetros en la red (4M, en comparación con AlexNet con 60M). Además, este documento utiliza Average Pooling en lugar de capas totalmente conectadas en la parte superior de ConvNet, eliminando una gran cantidad de parámetros que no parecen importar mucho. También hay varias versiones de seguimiento de GoogLeNet, la más reciente Inception-v4.
VGGNet. El subcampeón en ILSVRC 2014 fue la red de Karen Simonyan y Andrew Zisserman que se conoció como VGGNet. Su principal contribución fue mostrar que la profundidad de la red es un componente crítico para un buen rendimiento. Su mejor red final contiene 16 capas CONV / FC y, atractivamente, presenta una arquitectura extremadamente homogénea que solo realiza circunvoluciones 3x3 y agrupación 2x2 desde el principio hasta el final. Su modelo preentrenado está disponible para uso plug and play en Caffe. Una desventaja de VGGNet es que es más caro de evaluar y utiliza mucha más memoria y parámetros (140M). La mayoría de estos parámetros se encuentran en la primera capa totalmente conectada, y desde entonces se descubrió que estas capas FC se pueden eliminar sin degradar el rendimiento, lo que reduce significativamente el número de parámetros necesarios.
ResNet. Residual Network desarrollado por [Kaiming et al., 2015] fue el ganador de ILSVRC 2015. Cuenta con conexiones de salto especiales y un uso intensivo de la normalización por lotes. A la arquitectura también le faltan capas totalmente conectadas al final de la red. ResNets son actualmente modelos de red neuronal convolucional de última generación y son la opción predeterminada para usar ConvNets en la práctica (a partir del 10 de mayo de 2016).

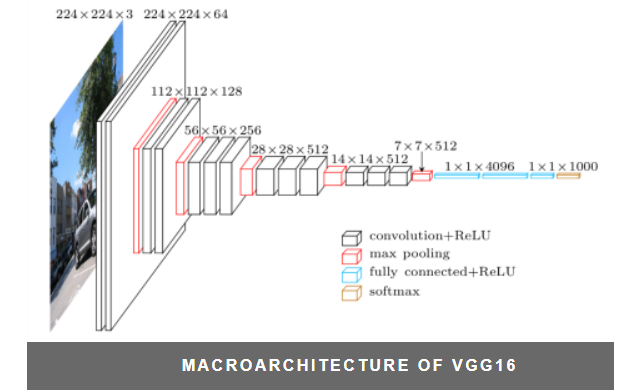
Esquema de la arquitectura VGGNet#

El modelo logra una precisión de prueba del 92,7 % entre los cinco primeros en ImageNet, que es un conjunto de datos de más de 14 millones de imágenes pertenecientes a 1000 clases. Dentro del modelo VGGNet se implementa la arquitectura VGG16:

Redes Residuales Profundas#

Las Redes Residuales Profundas (ResNets) consisten en muchas “Unidades Residuales” apiladas. Cada unidad (ver la siguiente figura) puede expresarse de forma general:

\[y_l = h(x_l) + F(w_l, W_l)\]

\[x_{l+1}=f(y_l)\]

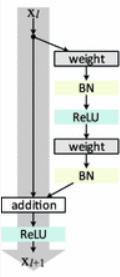
Dónde \(x_l\) y \(x_{l+1}\) son entradas y salidas de la unidad \(l\)-ésima, \(F\) es una función residual, \(h(x_l)=x_l\) es un mapeo de identidad y \(f\) es la función ReLU.

Para un mayor detalle y por ejemplo profundizar en la retropropagación de las ResNets consultar el capitulo de Kaiming:

https://link.springer.com/chapter/10.1007/978-3-319-46493-0_38

Ver también: https://pytorch.org/hub/pytorch_vision_resnet/

Entrenamiento de una red convolucional#

En cada capa de la red convolucional tendrá lugar, según tipología, un proceso de filtro convolucional, agrupación o ponderación lineal seguido de una activación. Todo ello constituye el paso adelante o proceso forward de la red. Para una red ya entrenada, el proceso forward permite obtener las predicciones.

El entrenamiento de la red requiere un proceso de retropropagación o backpropagation. Las capas finales que tienen que clasificar los patrones que han extraido las capas convolucionales son capas densas, como el perceptron o completamente conectadas (“full connected”). Puede haber 2 o 3 capas densas y en ellas el cálculo de los gradientes delta y el ajuste de las matrices W por su gradiente se realiza tal cual se ha comentado en el perceptron.

El bloque de capas densas, acabará propagando una matriz \(\Delta\) que se usará para obtener el gradiente y entrenar sus Filtros y Bias y propagar un \(\Delta\) a su vez a la capa anterior. Dependiendo del tipo de capa el proceso de forma esquemática será así:

Capa de aplanado#

La capa de aplanado se situa al final del proceso de convolución y tiene por objeto cambiar la dimensión de los tensores para que los procesen las capas densas. La función forward tiene que convertir un tensor de dimensión (n, c, b, h) en bidimensional (n, c*b*h) = (n, m) para cederle al bloque de capas densas. Por tanto la retropropagación recibirá una matriz \(\Delta_{n,m}^l\) bidimensional y tiene que recolocarla a tamaño \(\Delta_{n,c,b,h}^{l-1}\). Estás capas no tienen configuración dinámica y no tiene que ajustar ninguna matriz W.

Capa de Agrupación#

Las capas de agrupación (maxpooling) tienen también una configuración estática, el parámetro p de reducción de escala y la regla de agrupación, no hay matriz W entrenable. En la retropropagación sólo hay que progragar la matriz \(\Delta^l\) recibida para obtener la matriz \(\Delta^{l-1}\). El tamaño de \(\Delta^{l-1}\) se incrementará según la inversa de la escala p y la obtención de los \(\delta_{ij}^{l-1}\) a partir de \(\delta_{ij}^l\) seguirá una regla inversa. Por ejemplo si p=2 y se tiene agrupación por máximo, se repetirá cada valor \(\delta_{ij}^l\) en una región 2x2 de \(\Delta^{l-1}\).

Capa de convolución#

Entrenamiento: conocidas las matrices \(A^{l-1}\) y \(\Delta^l\) y considerando las dimensiones del filtro convolucional \(W^l\) hay que moverse por \(A^{l-1}\) multiplicando sus regiones por cada uno de los escalares \(\delta^l_{ij}\). El resultado es una matriz (\(\frac{\partial{C}}{\partial{W^l}}\)), de la misma dimensión que \(W^l\) a la que se acumula para optimizarla:

\[W^l \leftarrow -\eta \frac{\partial{C}}{\partial{W^l}}\]

La obtención de \(\frac{\partial{C}}{\partial{W^l}}\) es como se muestra en el siguiente gráfico (donde se supone \(W^l\) un filtro \(3\times 3\), \(A^{l-1} = [x_{ij}]\) con dimensión \(4\times 4\) y \(\Delta^l\) es dimensión \(2\times 2\)):

Nueva propagación: para obtener \(\Delta^{l-1}\) desde \(W^l\) y \(\Delta^l\), aplicando lo que se denomina una convolución traspuesta. El filtro \(W^l\) se combina sobre cada \(\delta^l_{ij}\) para obtener la matriz \(\Delta^{l-1}\) de la forma en que se explica en el siguiente gráfico:

Y continuaría así:

La convolución traspuesta existe como método en la arquitectura pytorch y además de ejecutarse internamente en el proceso de entrenamiento, se usa para modelos más avanzados como forma de trasladar tensores de una escala inferior a una superior dentro del proceso forward.

https://pytorch.org/docs/stable/generated/torch.nn.ConvTranspose2d.html

Note

El gradiente delta se propaga en una capa convolucional usando un filtro convolucional transpuesto.

Observaciones: En el cuaderno “Maqueta de red neuronal convolucional” se realiza una justificación de las anteriores operaciones convolucionales en un caso particular; sin padding ni strike, pero que resulta suficientemente general.

Otras consideraciones#

Función de pérdida (Loss Function) o de Coste: La función de pérdida más habitual es la entropia cruzada que va asociada con el uso de la función de activación softmax en la última capa.

La función softmax a partir del vector ponderación lineal \(\bar{z}\) obtiene una activación a un vector probabilidad \(\bar{p}\), donde cada elemento toma el valor:

\[p_i = \frac{e^{z_i}}{\sum_j e^{z_j}}\]

Y la función de pérdida cross_entropy entre \(\bar{p}\) y el valor real de entrenamiento \(\bar{y}\)

\[p_i = -\sum_j y_j \cdot ln(p_j)\]

Tiene la ventaja que en combinación con softmax da un valor del gradiente delta muy simple para la última capa (L):

\[\frac{\partial C}{\partial \bar{z^L}}=\bar{\delta^L} = \bar{p} - \bar{y}\]

https://pytorch.org/docs/stable/nn.html#loss-functions

Optmizador que hace referencia en la manera en que se ajustan los pesos y bias para optimizar la red.

En el gradiente descenso se aplican los gradientes usando un ratio de entrenamiento \(\eta\).

El gradiente descenso estocástico muestrea observaciones en un conjunto de entrenamiento de gran dimensión.

El optimizador Adam aplica una tasa de entrenamiento variable que se adapta automáticamente en las distintas capas de la arquitectura.

Ejercicio práctico de entrenamiento de un conjunto de imagenes usando convoluciones#

El manejo de mapas implica pasar de usar matrices como modelo de datos a tensores que son matrices de varias dimensiones. Los costes computacionales del entrenamiento de una red convolucional profunda con un conjunto de entrenamiento con valores \(N\) alto es muy elevado. Todo ello lleva a ser más práctico usar una arquitectura de desarrollo como Pytorch en lugar de sk-learn y usar una arquitectura de ejecución GPU en lugar de CPU. Este cuaderno está preparado para usarse en Google Colaboratory, donde se puede realizar un ejecución gratuita en GPU.

PyTorch es una biblioteca de aprendizaje automático de código abierto basada en la biblioteca de Torch, utilizado para implementar aplicaciones de visión artificial o procesamiento de lenguajes naturales. Desarrollado por el Laboratorio de Investigación de Inteligencia Artificial4 de Facebook (FAIR).Es un software libre y de código abierto liberado bajo la Licencia Modificada de BSD. A pesar de que la interfaz de Python está más pulida y es el foco principal del desarrollo, PyTorch también tiene una interfaz en C++.

Varios software de Aprendizaje Profundo están construidas utilizando PyTorch, como Tesla Autopilot, Uber’s Pyro, HuggingFace’s Transformers, PyTorch Lighting, y Catalyst.

PyTorch proporciona dos características de alto nivel:

Computación de tensores (como NumPy ) con una aceleración fuerte a través de unidades de procesamientos gráficos (GPU).
Redes neuronales profundas construidas en un sistema de diferenciación automática de bases de datos.

https://pytorch.org/

Comprendido el funcionamiento de sk-learn, el diseño de una red neuronal en Pytorch requiere los siguientes pasos básicos:

Los datos se estructuran en tensores de 4 dimensiones (\(N, C, B, H\)) para manejar imagenes bidimensionales (\(B, H\)). Siendo \(N\) el número de ejemplos del lote o de un conjunto completo de entrenamiento, \(C\) es el número de canales de entrada (3 para RGB) o la profundidad de mapas de cada capa.
Hay que definir una clase con la estructura de las capas de la red. La clase tendrá un constructor (Init) y un método forward. Crearemos un objeto llamando al constructor. Por ejemplo: model = CNN_long().
Hay que especificar la función de pérdida y el método de optimización.
El entrenamiento requerirá hacer un bucle por época donde se extraigan 1 a 1 los lotes del conjunto de entrenamiento y se vayan calculando las pérdidas y entrenando la red. Es un proceso estándar aunque algo más abierto que en sk-learn.
El modelo entrenado se puede guardar en fichero. Y una vez guardado es posible su recuperación para no tener que repetir el entrenamiento.

Modos de ejecución del cuaderno#

El cuaderno tiene una serie de variables booleanas que le permite ejecutarlo de diferentes maneras:

googleColaboratory : estando a True activará las opciones de acceso a Drive de Google y a la ejecución CUDA de Google Colaboratory.
entrenamiento : estando a True ejecuta el entrenamiento y guarda los datos a fichero en la carpeta data ya sea en Drive o local. Si está a False recupera la configuración de fichero existente en data.
resNet : estando a True se ejecuta sobre el modelo definido en class ResNet(nn.Module) que implementa una red residual. Si está a False carga un modelo en función del valor de la variable convolucionProfunda.
convolucionProfunda : Si resNet está a False y aquí aparece True implementa class CNN_long(nn.Module) con 3 bloques y hasta 6 convoluciones. En ella se presenta un estilo muy simple de programación de Pytorch basado en el uso de nn.Sequential. Si está a False se implementa class CNN_short(nn.Module) con sólo 2 convoluciones.

El entrenamiento de un modelo CNN_short es viable en una máquina CPU como Windows. Para el resto de modelos lo recomendable es una ejecución en una máquina con capacidad GPU. Google Colaboratory tiene un entorno libre que permite hacerlo manteniendo la sesión activa de forma manual. Con una cuenta de pago sería posible hacer esta ejecución en un segundo plano.

Abrir este cuaderno en Google Colab

import glob, os
import numpy as np
from PIL import Image
from IPython import display
import matplotlib.pyplot as plt
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transforms
import torch
import torch.nn as nn
from torch.autograd import Variable
from tqdm import tqdm

Se definen los parámetros de ejecución

googleColaboratory = False
entrenamiento = False
convolucionProfunda = False
resNet = False
if googleColaboratory:
    import google as goo

Carga de Datos#

PyTorch tiene dos primitivas para trabajar con bases de datos conocidas para hacer pruebas: torch.utils.data.DataLoader y torch.utils.data.Dataset.

Dataset almacena los ejemplos y sus correspondientes etiquetas, y DataLoader genera un iterable sobre el conjunto de datos.

Se utiliza la base de datos en línea CIFAR10 con 50.000 imagenes de entrenamiento de 10 clases distintas y 10.000 imagenes para prueba:

https://pytorch.org/tutorials/beginner/blitz/cifar10_tutorial.html

Las imágenes en CIFAR-10 tienen un tamaño de 3x32x32, es decir, imágenes en color de 3 canales de 32x32 píxeles de tamaño.

La base de datos es accesible desde torchvision.datasets

if googleColaboratory:
    goo.colab.drive.mount('/content/drive/')

Se visualizan algunas de las imagenes cargadas

from torchvision.utils import make_grid
for ix in range(3):
  for images, _ in trainloader:
    plt.figure(figsize=(6,3))
    plt.axis('off')
    plt.imshow(make_grid(images, nrow=16).permute((1, 2, 0)))
    break

_images/9bed229457c2040b076e9f32a124056974d6e9b3126006de9ea0e238e64bc612.png

_images/1b3340dc72ba274ac496c800c9a532766c05c34a9bc84d9b331afeaa705a9a8f.png

_images/7e02388d60581fcfb8e72aea953c02c3e920350b71097300b8b576839d902a4e.png

Clases con la definición de la Red#

Definición de la red residual (ResNet)#

La red está formada por la repetición de un bloque similar (ResidualBlock). El bloque está formado por una secuencia:

\[[CONV][BN][ReLU][CONV][BN]\]

Las convoluciones empleadas son todas de tamaño de filtro 3, salto 1 (en el primer bloque o layer y 2 en el resto) y padding o relleno a ceros 1. Los bloques residuales se integran en 3 capas o layers. La estructura de la red de convolución completa usando los bloques es:

\[[CONV][BN][ReLU][LAYER1][LAYER2][LAYER3][POOL][FC]\]

La estructura aparece explicitamente en el cuaderno trás hacer print(model).

El paso \([BN]\) es una Normalización (restando la media \(\mu\) y dividiendo por la desviación típica \(\sigma\))

Se utiliza una única capa conectada entre el vector aplanado el número de etiquetas del modelo.

La acumulación del valor residual se hace en cada bloque en la instrucción out += residual, copiandose el valor x existente al principio.

Pytorch incluye en línea unas definiciones de ResNet:

https://pytorch.org/hub/pytorch_vision_resnet/

Se puede descargar el modelo entrenado o no. El no entrenado puede utilizarse para un entrenamiento propio. Lo único tener en cuenta que el modelo devuelve hasta 1000 clases en salida. Si se usan 10 como en CIFAR10, el puntuaje máximo estará en los 10 primeros valores de esos 1000

Show code cell content Hide code cell content

# 3x3 convolution
def conv3x3(in_channels, out_channels, stride=1):
    return nn.Conv2d(in_channels, out_channels, kernel_size=3, 
                     stride=stride, padding=1, bias=False)

# Residual block
class ResidualBlock(nn.Module):
    def __init__(self, in_channels, out_channels, stride=1, downsample=None):
        super(ResidualBlock, self).__init__()
        self.conv1 = conv3x3(in_channels, out_channels, stride)
        self.bn1 = nn.BatchNorm2d(out_channels)
        self.relu = nn.ReLU(inplace=True)
        self.conv2 = conv3x3(out_channels, out_channels)
        self.bn2 = nn.BatchNorm2d(out_channels)
        self.downsample = downsample

    def forward(self, x):
        residual = x
        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)
        out = self.conv2(out)
        out = self.bn2(out)
        if self.downsample:
            residual = self.downsample(x)
        out += residual
        out = self.relu(out)
        return out

# ResNet
class ResNet(nn.Module):
    def __init__(self, block, layers, num_classes=10):
        super(ResNet, self).__init__()
        self.in_channels = 16
        self.conv = conv3x3(3, 16)
        self.bn = nn.BatchNorm2d(16)
        self.relu = nn.ReLU(inplace=True)
        self.layer1 = self.make_layer(block, 16, layers[0])
        self.layer2 = self.make_layer(block, 32, layers[1], 2)
        self.layer3 = self.make_layer(block, 64, layers[2], 2)
        self.avg_pool = nn.AvgPool2d(8)
        self.fc = nn.Linear(64, num_classes)

    def make_layer(self, block, out_channels, blocks, stride=1):
        downsample = None
        if (stride != 1) or (self.in_channels != out_channels):
            downsample = nn.Sequential(
                conv3x3(self.in_channels, out_channels, stride=stride),
                nn.BatchNorm2d(out_channels))
        layers = []
        layers.append(block(self.in_channels, out_channels, stride, downsample))
        self.in_channels = out_channels
        for i in range(1, blocks):
            layers.append(block(out_channels, out_channels))
        return nn.Sequential(*layers)

    def forward(self, x):
        out = self.conv(x)
        out = self.bn(out)
        out = self.relu(out)
        out = self.layer1(out)
        out = self.layer2(out)
        out = self.layer3(out)
        out = self.avg_pool(out)
        out = out.view(out.size(0), -1)
        out = self.fc(out)
        return out

# Se crea un modelo CNN
#if googleColaboratory:
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') #training with either cpu or cuda

    
if resNet:
    if googleColaboratory:
      model = ResNet(ResidualBlock, [2, 2, 2]).to(device)  
    else:
        model = ResNet(ResidualBlock, [2, 2, 2])
elif convolucionProfunda:
  model = CNN_long()
else:
  model = CNN_short()
if googleColaboratory:
  model = model.to(device=device) #to send the model for training on either cuda or cpu
  
print(model)

CNN_short(
  (conv1): Conv2d(3, 6, kernel_size=(5, 5), stride=(1, 1))
  (pool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

Especificar la Función de Pérdida y el Optimizador#

http://pytorch.org/docs/stable/nn.html#loss-functions

http://pytorch.org/docs/stable/optim.html

import torch.optim as optim

# Se especifica la función pérdida
loss_func = nn.CrossEntropyLoss()

# Se especifica el optimizador
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
#optimizer = optim.Adam(model.parameters(), lr=0.001)

Entrenamiento de la red#

Hay que observar como la pérdida en entrenamiento y validación disminuye con el tiempo; si la pérdida de validación aumenta alguna vez, indica un posible sobreajuste.

#from torch.autograd import Variable
num_epochs = 10
model.train()

lineasTraza = int(len(trainloader)/20)+1
numlineas = 0
#pbar = tqdm(range(num_epochs))
# Train the model
for epoch in range(num_epochs):
#for epoch in pbar:
    if not entrenamiento:
      print("No habilitada la opción de entrenamiento")
      break
    correct = 0
    total = 0
    for images, labels in trainloader:
        images = images.to(device=device)
        labels = labels.to(device=device)
            
        # gives batch data, normalize x when iterate train_loader
        output = model(images)
        loss = loss_func(output, labels)
        pred_y = torch.max(output, 1)[1].data.squeeze()
        correct += (pred_y == labels).sum().item()
        total +=float(labels.size(0))
        # clear gradients for this training step   
        optimizer.zero_grad()           
            
        # backpropagation, compute gradients 
        loss.backward()    
        # apply gradients             
        optimizer.step()  
        numlineas+=1
        if numlineas == lineasTraza:
            print('*', end='')
            numlineas=0
            
    print ('Época [{}], Accuracy-Entrenamiento {:.4f}'.format(epoch + 1, 100*correct/total))

No habilitada la opción de entrenamiento

Se hace un back-up del modelo generado#

filename = "cifar10_profunda.pt" if convolucionProfunda else "cifar10_short.pt"
if resNet: filename = "cifar10_resnet.pt"
filename = "/content/drive/My Drive/Colab Notebooks/data/" + filename if googleColaboratory else "data/" + filename
if entrenamiento:
    print("Backup al fichero=", filename)
    torch.save(model.state_dict(), filename)
    if googleColaboratory:
      goo.colab.files.download(filename)
else:
    print("No habilitado Backup del fichero")

No habilitado Backup del fichero

Recuperación del modelo desde el archivo de back-up#

if entrenamiento: 
    print('No activada la recuperación en modo entrenamiento')
else:
    device = torch.device('cpu')
    if googleColaboratory:
        device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') #training with either cpu or cuda
    model = CNN_long() if convolucionProfunda else CNN_short()
    if resNet: model = ResNet(ResidualBlock, [2, 2, 2]).to(device) 
    filename = "cifar10_profunda.pt" if convolucionProfunda else "cifar10_short.pt"
    if resNet: filename = "cifar10_resnet.pt"
    filename = "/content/drive/My Drive/Colab Notebooks/data/" + filename if googleColaboratory else "data/" + filename
    print("Fichero cargado=", filename)
    if googleColaboratory:
        model.load_state_dict(torch.load(filename, map_location=torch.device('cpu'))) #recovery trained model
    else:
        model.load_state_dict(torch.load(filename, map_location=torch.device('cpu'))) #recovery trained model
    model.eval()
    print(model)

Fichero cargado= data/cifar10_short.pt
CNN_short(
  (conv1): Conv2d(3, 6, kernel_size=(5, 5), stride=(1, 1))
  (pool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

Se evalua el modelo contra el conjunto de validación#

model.eval()
with torch.no_grad():
    correct = 0
    total = 0
    for images, labels in testloader:
        images = images.to(device=device)
        labels = labels.to(device=device)
        test_output = model(Variable(images))
        pred_y = torch.max(test_output, 1)[1].data.squeeze()
        #accuracy = (pred_y == labels).sum().item() / float(labels.size(0))
        correct += (pred_y == labels).sum().item()
        total +=float(labels.size(0))
    accuracy=100*correct/total
print('El Acierto en los 10.000 ejemplos de prueba es : %.2f %%' % accuracy)

El Acierto en los 10.000 ejemplos de prueba es : 58.66 %

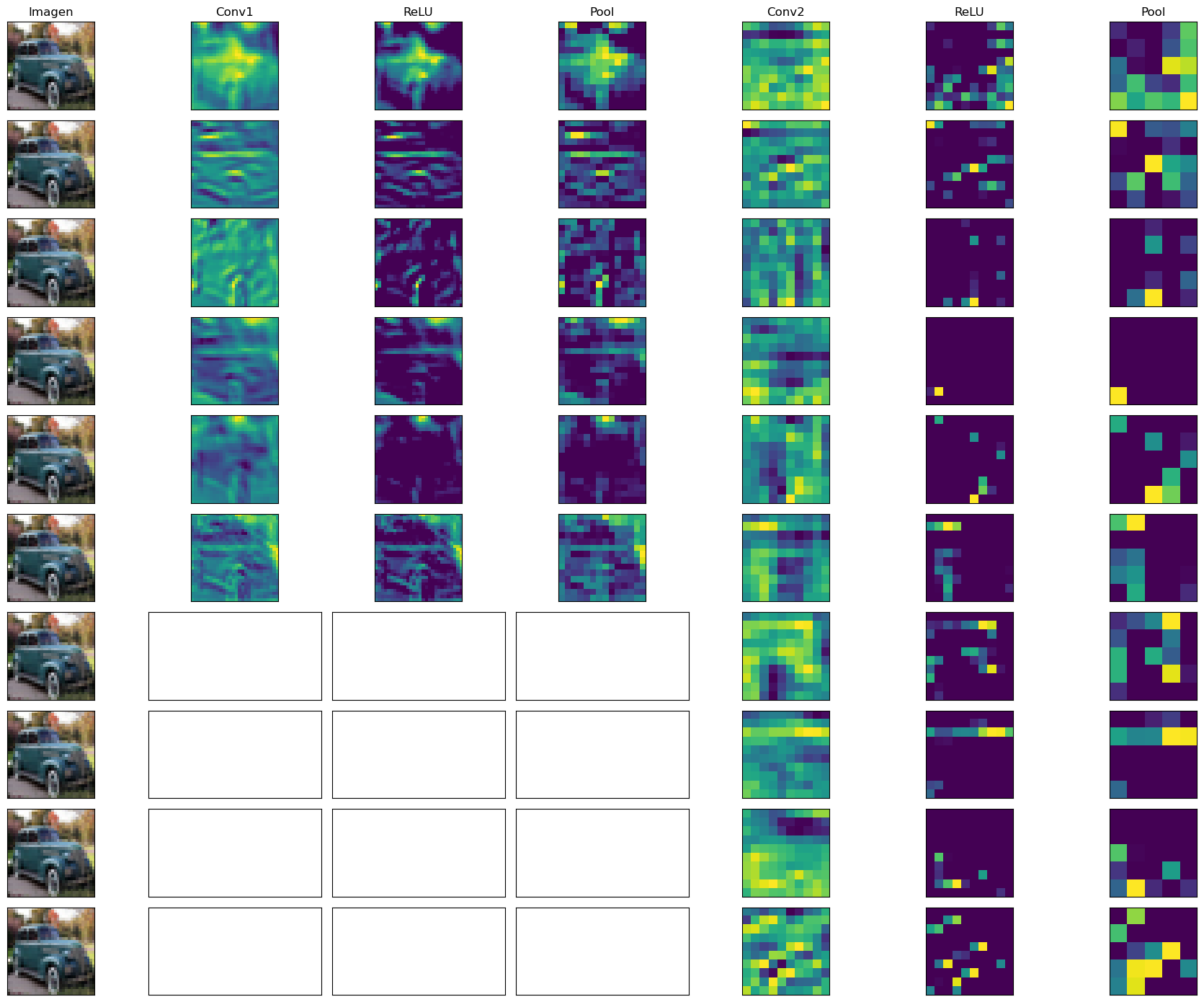
Se visualiza el aspecto de los mapas de las convoluciones#

El dibujo sólo está preparado para modo CPU. Una vez entrenado en GPU y volcado a fichero, recuperar en CPU y dibujar los mapas.

Sólo tiene un sentido el color de las imagenes. El color de los mapas no es significativo, pues no son dibujos RGB en si mismo, sino extracciones de características

import matplotlib.pyplot as plt
lote_image, lote_label = next(iter(testloader))
lote_mapa1 = model.conv1(lote_image)

model.conv1.weight.size()

torch.Size([6, 3, 5, 5])

model.conv1.weight[0][0]

tensor([[-0.1175, -0.1575, -0.0339,  0.0565,  0.0824],
        [-0.1093, -0.2938, -0.1184, -0.1067, -0.1209],
        [-0.3021, -0.3066, -0.3274, -0.1769, -0.1177],
        [-0.3013, -0.4303, -0.1758, -0.1064, -0.2395],
        [-0.4223, -0.4339, -0.3206, -0.1417, -0.2228]],
       grad_fn=<SelectBackward0>)

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
lote_image, lote_label = next(iter(testloader))
if resNet: 
  lote_mapa1 = model.conv(lote_image)
  lote_mapa2 = model.bn(lote_mapa1)
  lote_mapa3 = model.relu(lote_mapa2)
  lote_mapa4 = model.layer1[0].conv1(lote_mapa3)
  lote_mapa5 = model.layer1[0].bn1(lote_mapa4)
  lote_mapa6 = model.layer1[0].relu(lote_mapa5)
  lote_mapa7 = model.layer1[0].conv2(lote_mapa6)
  lote_mapa8 = model.layer1[0].bn2(lote_mapa7)
  lote_mapa9 = model.layer1[1].conv1(lote_mapa8)
  lote_mapa10 = model.layer1[1].bn1(lote_mapa9)
  lote_mapa11 = model.layer1[1].relu(lote_mapa10)
  lote_mapa12 = model.layer1[1].conv2(lote_mapa11)
  lote_mapa13 = model.layer1[1].bn2(lote_mapa12)
  lote_mapa14 = model.layer2[0].conv1(lote_mapa13)
  lote_mapa15 = model.layer2[0].bn1(lote_mapa14)
elif convolucionProfunda:
  conv1 = nn.Conv2d(3, 32, kernel_size=3, padding=1)
  lote_mapa1 = conv1(lote_image)
  lote_mapa2 = F.relu(lote_mapa1)
  conv2 = nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1)
  lote_mapa3 = conv2(lote_mapa2)
  lote_mapa4 = F.relu(lote_mapa3)
  pool = nn.MaxPool2d(2, 2)
  lote_mapa5 = pool(lote_mapa4)
  conv3 = nn.Conv2d(64, 128, kernel_size=3, stride=1, padding=1)
  lote_mapa6 = conv3(lote_mapa5)
  lote_mapa7 = F.relu(lote_mapa6)
  conv4 = nn.Conv2d(128, 128, kernel_size=3, stride=1, padding=1)
  lote_mapa8 = conv4(lote_mapa7)
  lote_mapa9 = F.relu(lote_mapa8)
  lote_mapa10 = pool(lote_mapa9)
  conv5 = nn.Conv2d(128, 256, kernel_size=3, stride=1, padding=1)
  lote_mapa11 = conv5(lote_mapa10)
  lote_mapa12 = F.relu(lote_mapa11)
  conv6 = nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1)
  lote_mapa13 = conv6(lote_mapa12)
  lote_mapa14 = F.relu(lote_mapa13)
  lote_mapa15 = pool(lote_mapa14)
else:
  lote_mapa1 = model.conv1(lote_image)
  lote_mapa2 = F.relu(lote_mapa1)
  lote_mapa3 = model.pool(lote_mapa2)
  lote_mapa4 = model.conv2(lote_mapa3)
  lote_mapa5 = F.relu(lote_mapa4)
  lote_mapa6 = model.pool(lote_mapa5)
image = lote_image[0]  ## Se coge la primera imagen del lote
mapa1 = lote_mapa1[0]
mapa2 = lote_mapa2[0]
mapa3 = lote_mapa3[0]
mapa4 = lote_mapa4[0]
mapa5 = lote_mapa5[0]
mapa6 = lote_mapa6[0]
if convolucionProfunda or resNet:
  mapa7 = lote_mapa7[0]
  mapa8 = lote_mapa8[0]
  mapa9 = lote_mapa9[0]
  mapa10 = lote_mapa10[0]
  mapa11 = lote_mapa11[0]
  mapa12 = lote_mapa12[0]
  mapa13 = lote_mapa13[0]
  mapa14 = lote_mapa14[0]
  mapa15 = lote_mapa15[0]
label = int(lote_label[0])
numCols = 16 if convolucionProfunda or resNet else 7
fig, ax = plt.subplots(nrows=10, ncols=numCols, figsize=(18,14))
#ax = ax.flatten()
if resNet:
  literales=['Imagen', 'Conv', 'Normal', 'ReLU', 'Conv', 'Normal', 'ReLU', 'Conv', 'Normal', 'Conv', 'Normal', 'ReLU', 'Conv', 'Normal', 'Conv', 'Normal', 'ReLU']
elif convolucionProfunda:
  literales=['Imagen', 'Conv1', 'ReLU', 'Conv2', 'ReLU', 'Pool', 'Conv3', 'ReLU', 'Conv4', 'ReLU', 'Pool', 'Conv5', 'ReLU', 'Conv6', 'ReLU', 'Pool']
else:
  literales=['Imagen', 'Conv1', 'ReLU', 'Pool', 'Conv2', 'ReLU', 'Pool']
for i in range(10):
    ax[i][0].imshow(image.numpy().transpose((1, 2, 0)))
    if i < mapa1.shape[0]:
        ax[i][1].imshow(mapa1[i].detach().numpy())
        ax[i][2].imshow(mapa2[i].detach().numpy())
        ax[i][3].imshow(mapa3[i].detach().numpy())
    ax[i][4].imshow(mapa4[i].detach().numpy())
    ax[i][5].imshow(mapa5[i].detach().numpy())
    ax[i][6].imshow(mapa6[i].detach().numpy())
    if convolucionProfunda or resNet:
      ax[i][7].imshow(mapa7[i].detach().numpy())
      ax[i][8].imshow(mapa8[i].detach().numpy())
      ax[i][9].imshow(mapa9[i].detach().numpy())
      ax[i][10].imshow(mapa10[i].detach().numpy())
      ax[i][11].imshow(mapa11[i].detach().numpy())
      ax[i][12].imshow(mapa12[i].detach().numpy())
      ax[i][13].imshow(mapa13[i].detach().numpy())
      ax[i][14].imshow(mapa14[i].detach().numpy())
      ax[i][15].imshow(mapa15[i].detach().numpy())
    for j in range(numCols):
        ax[i][j].set_yticks([])
        ax[i][j].set_xticks([])
        ax[0][j].set_title(literales[j])

#fig.suptitle('Imagen tipo ' + str(clases[label]), fontsize=16)
plt.tight_layout()
plt.show()

_images/61c4f1670a1247495587f52ffd423fb588d6baf40b0552329bb0a9e0e41f6ca2.png

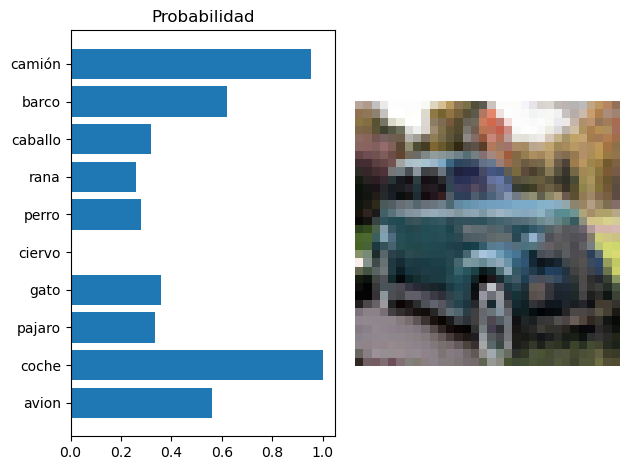
Se visualiza la predicción#

#b_x = Variable(lote_image)   # batch x
#output = model(b_x)
output = model(lote_image)
fig, (ax1, ax2) = plt.subplots( ncols=2)
y=output[0].detach().numpy()
y = (y - min(y))/(max(y)-min(y))
ax2.axis('off')
ax2.imshow(image.numpy().transpose((1, 2, 0)))
ax1.set_yticks(np.arange(10))
ax1.barh(np.arange(10), y)
ax1.set_yticklabels(clases)
ax1.set_title('Probabilidad')
plt.tight_layout()

_images/5e374733e8ff1ed207975dca90908d4617e8e20b5e633c370da33c09455ff3c4.png