Práctica 2. Clustering de regiones vinícolas#

En una práctica anterior ya utilizamos los datos de las características de unos vinos pertenecientes a tres bodegas italianas (fichero de datos wines o wine.csv que se puede encontrar en el libro de la asignatura.

En esta práctica vamos a aplicar un aprendizaje no supervisado como el que propone los mapas auto-organizativo de Kohonen para obtener un agrupamiento de los datos.

Cargar el paquete específico#

A continuación cargamos el paquete específico que vamos a usar en esta sección para trabajar con mapas auto-organizativos de Kohonen realizado en Python:

import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler

#!git clone https://github.com/cgg-upm/upm-dma-som
#!dir upm-dma-som\som
#!copy upm-dma-som\som\som.py .\*.*
#!copy upm-dma-som\som\utils.py .\*.*
Hide code cell content 
from som import som
from utils import somutils

Carga de los datos.#

Cargamos el archivo con data("wines") que ya contiene el nombre de cada columna y no incluye la primera de las columnas que indica la bodega a la que pertenecen los datos de cada instancia (fila).

En el caso de los mapas auto-organizativos, donde se va a establecer una relación de proximidad entre los atributos, es conveniente escalar los datos.

Estos datos provienen de

https://archive.ics.uci.edu/ml/datasets/Wine

# Se preparan las columnas a tratar
df_wine = pd.read_csv('data/wine.csv', header=None)
df_wine.columns = ['label', 'alcohol',
    'malic acid', 'ash',
    'ash alkalinity',
    'magnesium', 'tot. phenols',
    'flavanoids', 'non-flav. phenols',
    'proanth',
    'col. int.', 'col. hue',
    'OD ratio'
    ,'proline']
# Se borra la columna de la etiqueta
df_wine = df_wine.drop('label', axis=1)
df_wine.head()
alcohol malic acid ash ash alkalinity magnesium tot. phenols flavanoids non-flav. phenols proanth col. int. col. hue OD ratio proline
0 14.23 1.71 2.43 15.6 127 2.80 3.06 0.28 2.29 5.64 1.04 3.92 1065
1 13.20 1.78 2.14 11.2 100 2.65 2.76 0.26 1.28 4.38 1.05 3.40 1050
2 13.16 2.36 2.67 18.6 101 2.80 3.24 0.30 2.81 5.68 1.03 3.17 1185
3 14.37 1.95 2.50 16.8 113 3.85 3.49 0.24 2.18 7.80 0.86 3.45 1480
4 13.24 2.59 2.87 21.0 118 2.80 2.69 0.39 1.82 4.32 1.04 2.93 735 
"Número de filas :",  df_wine.values.shape[0], " Número de columnas :", df_wine.values.shape[1]

('Número de filas :', 178, ' Número de columnas :', 13)

scaler = StandardScaler()
X = df_wine.to_numpy()
X_std = scaler.fit_transform(X)
X_std.shape, X.shape

((178, 13), (178, 13))

df=pd.DataFrame(X_std)
columnas = ['alcohol','malic acid','ash',
    'ash alkalinity',
    'magnesium', 'tot. phenols',
    'flavanoids', 'non-flav. phenols',
    'proanth',
    'col. int.', 'col. hue',
    'OD ratio'
    ,'proline']
df.columns = columnas

df.head()
alcohol malic acid ash ash alkalinity magnesium tot. phenols flavanoids non-flav. phenols proanth col. int. col. hue OD ratio proline
0 1.518613 -0.562250 0.232053 -1.169593 1.913905 0.808997 1.034819 -0.659563 1.224884 0.251717 0.362177 1.847920 1.013009
1 0.246290 -0.499413 -0.827996 -2.490847 0.018145 0.568648 0.733629 -0.820719 -0.544721 -0.293321 0.406051 1.113449 0.965242
2 0.196879 0.021231 1.109334 -0.268738 0.088358 0.808997 1.215533 -0.498407 2.135968 0.269020 0.318304 0.788587 1.395148
3 1.691550 -0.346811 0.487926 -0.809251 0.930918 2.491446 1.466525 -0.981875 1.032155 1.186068 -0.427544 1.184071 2.334574
4 0.295700 0.227694 1.840403 0.451946 1.281985 0.808997 0.663351 0.226796 0.401404 -0.319276 0.362177 0.449601 -0.037874

Definir y entrenar el SOM#

La elección de la red bidimensional, tanto en lo que se refiere al número de neuronas como en tipo de entorno, depende del tipo de datos que se esté analizando. En este caso concreto, estamos tratando con instancias que contienen trece atributos y parece conveniente empezar con una malla de \(5 \times 5\) neuronas que denominaremos som_wine

nrows = 5
ncols = 5
dimensions = X_std.shape[1]
#dimensions = X.shape[1]
#vicinity = "rectangular"
vicinity = "hexagonal"
som_wine = som(nrows=nrows,
          ncols=ncols,
          dimension=dimensions,
          vicinity=vicinity)
som_wine.train_SOM(train_data=X_std,
              epochs=10)
Hide code cell output 
  0%|                                                                                                                                                     | 0/10 [00:00<?, ?it/s]

 60%|████████████████████████████████████████████████████████████████████████████████████▌                                                        | 6/10 [00:00<00:00, 47.78it/s]

100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 10/10 [00:00<00:00, 49.11it/s]



<som.som at 0x1ac2ba53a10>

Resumen del mapa SOM#

Comandos específicos de este paquete permiten obtener un resumen de las caracterísiticas del mapa generado. En concreto, la asignación de cada instancia a una neurona del SOM.

redXY = somutils.getRedSOM(pSom=som_wine)
df=pd.DataFrame(redXY.T)
cols_=[]
for i in range(som_wine.nrows):
    for j in range(som_wine.ncols):
        cols_.append("N(" + str(i) + "," + str(j)+")")
df.columns=cols_
df.insert(loc = 0, column = '', value = ['x','y'])
pd.set_option('display.max_columns', None)
df.head(len(df))
N(0,0) N(0,1) N(0,2) N(0,3) N(0,4) N(1,0) N(1,1) N(1,2) N(1,3) N(1,4) N(2,0) N(2,1) N(2,2) N(2,3) N(2,4) N(3,0) N(3,1) N(3,2) N(3,3) N(3,4) N(4,0) N(4,1) N(4,2) N(4,3) N(4,4)
0 x -0.87 0.87 2.6 4.33 6.06 -1.73 0.0 1.73 3.46 5.2 -0.87 0.87 2.6 4.33 6.06 -1.73 0.0 1.73 3.46 5.2 -0.87 0.87 2.6 4.33 6.06
1 y -1.50 -1.50 -1.5 -1.50 -1.50 0.00 0.0 0.00 0.00 0.0 1.50 1.50 1.5 1.50 1.50 3.00 3.0 3.00 3.00 3.0 4.50 4.50 4.5 4.50 4.50 
df=pd.DataFrame(som_wine.getCodes())
df.columns = columnas
df.head(len(df))
alcohol malic acid ash ash alkalinity magnesium tot. phenols flavanoids non-flav. phenols proanth col. int. col. hue OD ratio proline
0 1.118660 -0.439818 0.170988 -0.978464 0.390204 1.179482 1.258905 -0.663509 1.041480 0.598224 0.577160 0.645062 1.668355
1 0.823506 -0.451143 0.817574 -0.269501 0.778437 0.886280 0.923331 -0.317008 0.428948 0.232361 0.729886 0.575058 1.283498
2 -0.094426 -0.422711 0.890206 0.685920 1.102863 0.710904 0.775821 -0.298339 0.674127 -0.428259 0.708628 0.678341 0.178176
3 -0.927541 -0.666616 -0.383976 -0.151583 0.294839 0.295482 0.252228 -0.668582 0.681696 -0.765150 0.452518 0.451436 -0.417614
4 -0.926944 -0.016138 -0.891453 -0.070535 -0.677695 0.656616 0.566440 -0.501276 0.760950 -0.831100 0.132880 0.573395 -0.901375
5 1.124451 -0.265270 -0.131122 -1.101480 0.665591 1.011665 1.039798 -0.864737 0.688255 0.270879 0.161743 1.020413 0.844724
6 0.820392 -0.402517 0.029353 -0.889296 0.134550 0.573243 0.728417 -0.557741 0.291648 -0.008481 0.495416 0.716816 1.179795
7 0.289536 -0.304369 0.582758 -0.184226 0.311944 0.393630 0.543197 -0.500398 0.168165 -0.234072 0.508162 0.661107 0.616976
8 -0.533035 -0.264845 -0.152866 0.257915 0.077772 0.121004 0.183090 -0.253416 0.095137 -0.753254 0.439380 0.488752 -0.472090
9 -0.799355 -0.665380 -1.249432 -0.269835 -0.658554 -0.185267 -0.076114 -0.398579 -0.234780 -0.855090 0.667414 0.333695 -0.735274
10 0.806571 0.374124 -0.054972 -0.557881 0.300171 0.495446 0.547584 -0.532592 0.132454 0.186106 -0.108246 0.530386 0.706730
11 0.343145 0.080746 0.149751 -0.222048 0.217031 -0.040036 0.065763 -0.341570 -0.129419 0.116382 -0.091674 0.053389 0.418761
12 -0.315693 0.010514 0.148301 0.163566 0.253669 -0.430158 -0.295983 -0.265418 -0.291878 -0.340407 -0.042689 -0.127399 -0.163379
13 -0.642263 -0.281213 -0.344207 0.367332 -0.487977 -0.438740 -0.242682 0.118943 -0.355425 -0.732923 0.324115 0.074656 -0.659024
14 -1.133653 -0.637461 -0.119162 0.657924 -0.824077 -0.290002 -0.157568 0.406662 -0.245444 -1.001885 0.887965 0.165771 -0.819333
15 0.606440 0.568985 0.244826 0.188311 0.332009 -0.248212 -0.375925 -0.029910 -0.100340 1.067621 -0.879148 -0.538066 0.058477
16 0.347237 0.678939 0.161807 0.284593 0.124245 -0.634487 -0.731731 0.148098 -0.441458 0.975838 -1.008807 -0.863100 -0.123394
17 -0.106596 0.560684 -0.067107 0.185676 0.106180 -1.174343 -1.026848 -0.085842 -0.980505 0.362549 -0.987922 -1.116832 -0.297535
18 -0.515914 0.395111 -0.184756 0.230042 -0.249101 -1.024667 -0.853114 0.617788 -0.788149 -0.377206 -0.419476 -0.659460 -0.514577
19 -0.881068 0.066244 0.243498 0.718331 -0.677574 -0.793752 -0.431586 1.152861 -0.355837 -0.779553 0.096004 -0.164712 -0.745526
20 0.488421 0.697812 0.654223 0.937702 0.503631 -0.731395 -0.989713 0.321795 -0.184405 1.931283 -1.471377 -1.405892 -0.377290
21 0.319742 1.084054 0.070103 0.407846 -0.358215 -0.963284 -1.264209 0.811039 -0.664374 1.454207 -1.440817 -1.344643 -0.369515
22 0.051436 0.877738 -0.240270 0.318410 -0.354413 -1.229535 -1.338656 0.972707 -0.932370 0.440699 -1.077153 -1.237594 -0.439470
23 -0.209557 0.942480 0.469832 0.755944 -0.283836 -0.891864 -1.198824 1.410127 -1.001209 -0.080023 -0.491135 -0.904986 -0.473960
24 -0.474725 -0.251794 -0.052602 0.020604 -0.290433 -0.552042 -0.857826 1.475043 -1.108983 -0.370229 0.001621 -0.897555 -0.506219

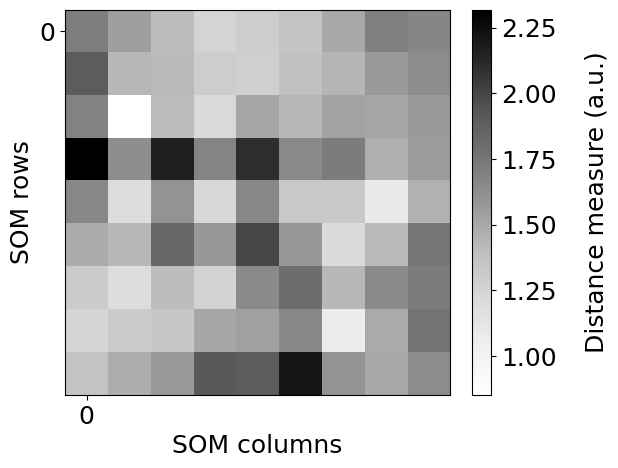
Dibujo de la matriz de distancias unificadas (U-Matrix)#

Contiene la distancia entre los nodos del SOM. En el gráfico a más intensidad hay una menor distancia entre las neuronas adyacentes. Para cada neurona se calcula la distancia entre ella y sus neuronas vecinas más próximas. Cuanto menor sea el resultado, más próxima estará la neurona con sus vecinas.

somutils.plot_u_matrix(pSom=som_wine, figsize=(7,5))
_images/61e324af45d71706b105935e6daaa7eb30ad69a7d957f1a3f62855b7d3196282.png

Número de instancias asociadas a cada neurona#

somutils.plot_neurPointsCount(pSom=som_wine, figsize=(7,5))
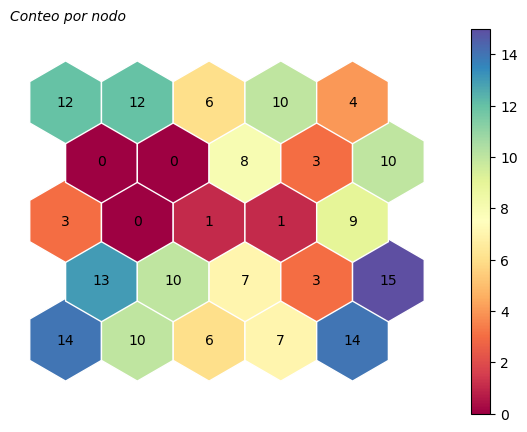
_images/12eed5f0c1360823702d577fe114c579b631583c9ad343e8432835b30a561c1f.png

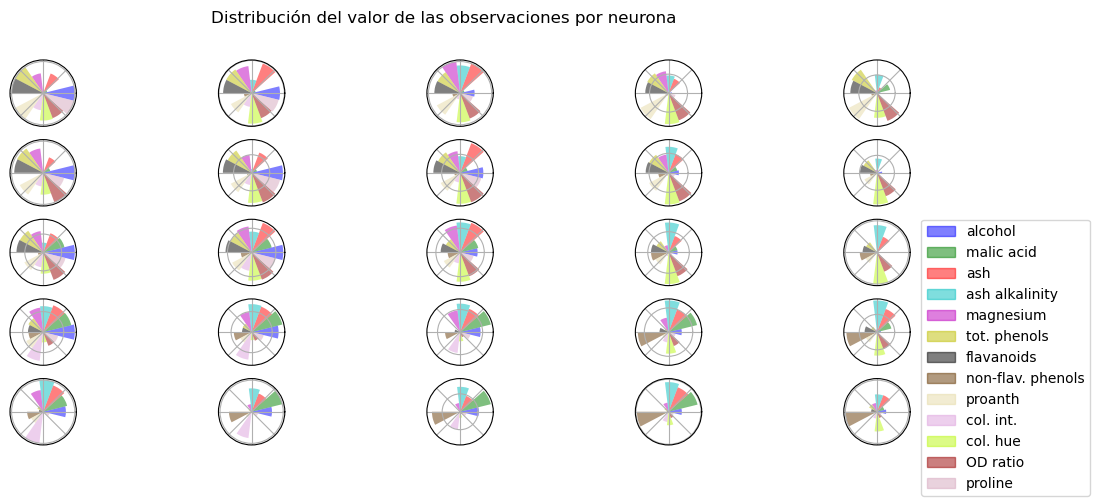
Gráfico de códigos#

Otro gráfico muy útil para entender el agrupamiento de los datos es el que representa la distribución de los atributos en cada neurona, esto es el vector representativo al que ha convergido cada neurona después del entrenamiento. Haz esta figura y comenta cómo están agrupados los datos en wine.csv.

somutils.plot_valuesMap(pSom=som_wine, labels=columnas, figsize=(13,5))
_images/05ebdbe4e0d2b5879745c7e8843c7c37f03c0f6da263b44b0e935797929681d9.png

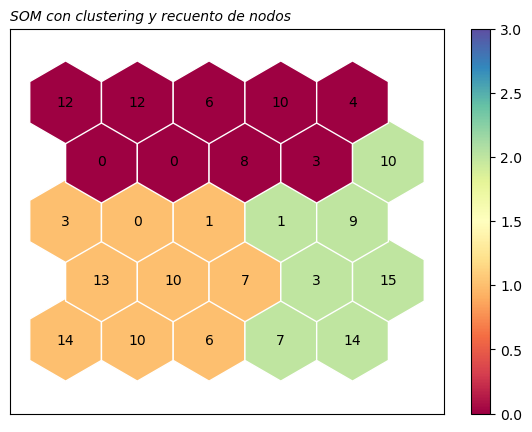
Clustering#

Podemos realizar un clustering jerárquico con la función plot_Cluster_hexagon usando las distancias entre los vectores prototípicos de las neuronas y añadirlo a la representación.

somutils.plot_Cluster(pSom=som_wine, n_clusters=3, figsize=(7,5))
_images/6a824b6145d1358cb9e97798dcda9ef0fe407d455854d13aca64b5f6dd178e6b.png 
som_wine.data_map[0][0]

[1, 21, 30, 31, 55, 60, 68, 71, 76, 94, 108, 110, 150, 158]