Maqueta de red neuronal convolucional

Maqueta de red neuronal convolucional#

import numpy as np
from tqdm import tqdm 
import pickle
import logging
from scipy import signal as sg

Configuración del proceso

entrenamiento=False

Redes convolucionales#

Izquierda: Una red neuronal normal de 3 capas. Derecha: Un ConvNet organiza sus neuronas en tres dimensiones (ancho, alto, profundidad), como se visualiza en una de las capas. Cada capa de un ConvNet transforma el volumen de entrada 3D en un volumen de salida 3D de activaciones neuronales. En este ejemplo, la capa de entrada roja contiene la imagen, por lo que su ancho y alto serían las dimensiones de la imagen, y la profundidad sería de 3 (canales rojo, verde, azul).

Una Arquitectura Convolucional tipo estará compuesta por las capas: [INPUT - CONV - RELU - POOL - FC]. Cuyo detalle es:

INPUT [bxhx3] contendrá los valores de píxeles raw de la imagen, en este caso una imagen de ancho b, altura h, y con tres canales de color R, G, B.
La capa CONV calculará la salida de las neuronas que están conectadas a las regiones locales en la entrada, cada una calculando un producto de punto entre sus pesos y una pequeña región a la que están conectadas en el volumen de entrada. Esto puede resultar en un volumen como [BxHxd] si decidimos usar d filtros. Los pesos que conectan los pixels localmente son compartidos y son aprendibles.
La capa RELU aplicará una función de activación por elementos, como el umbral \((max(0,x))\) en cero. Esto deja el tamaño del volumen sin cambios ([BxHxd]).
La capa POOL realizará una operación de downsampling a lo largo de las dimensiones espaciales (ancho, alto), lo que dará como resultado un volumen como [bxhxd], siendo (b,h) inferiores a (B,H). Esta capa no utiliza pesos aprendibles.
La capa FC o densa (es decir, totalmente conectada) calculará los puntajes de clase, lo que resultará en un volumen de tamaño [1x1xK], donde cada uno de los K números corresponde a un puntaje de clase, entre las K categorías del conjunto. Al igual que con las redes neuronales ordinarias y como su nombre indica, cada neurona en esta capa estará conectada a todos los números en el volumen anterior.

Fundamento teórico#

Una red neuronal se puede considerar (LeCun et al.; 1998) un sistema construido como una cascada de módulos, cada uno de los cuales implementa una función

\[X_l = F_l(W_l, X_{l-1})\]

Se toma \(l\) como el índicador de número de capa (layer en inglés).

Dónde \(X_l\) es un vector que representa la salida del módulo, \(W_l\) es el vector de los parámetros entrenables del módulo (y que forma parte del conjunto total \(W\)) y \(X_{l-1}\) es el vector de entrada al módulo (así como la salida del módulo previo).

Se ha implementado una maqueta naíf que implementa 4 tipos de capas: densa o perceptrón, convolucional, agrupación máxima (max-pooling) y aplanado. La capa densa con una programación matricial en numpy se implementa de acuerdo a la documentación previa. La capa convolucional se restringe a convoluciones 2D sin relleno a ceros y con salto 1. La agrupación máxima usa un paso único en ambas direcciones de la imagen. El aplanado es un simple cambio de formato para pasar de las capas convolucionales a las densas.

Al final de la última capa se aplica una función softmax para obtener las probabilidades de cada clase y la pérdida se calcula con una función de croos-entropy.

También se incorpora la optimación Adam que provee un ratio de aprendizaje modulado ([Kingma and Ba, 2014]).

El vector de datos de entrada \(X_0\) va a ser un tensor o matriz de 4 dimensiones (n, c, h, b), donde n representará el número de observaciones en el lote tratado, c el número de canales, h es la altura de la imagen y b es el ancho de la imagen.

Esta estructura de los vectores \(X_l\) se mantiene durante los procesos convolucionales y de agrupación, mientras que las capas densas manejan tensores de la forma (n, m), siendo n el número de observaciones tratadas y m las características de cada observación. Lógicamente, la capa de aplanado efectua reestructuración de las dimensiones con m = c * h * b.

En una capa convolucional los parámetros entrenables están formados por un filtro \(W_l\) cuyas dimensiones son (co, ci, f, f), donde co es el número de canales de salida (los canales del tensor \(X_l\)), ci es el número de canales de entrada (los canales del tensor \(X_{l-1}\)) y f es el tamaño del filtro. Además se incluye un parámetro de bias \(B_l\), que es un vector de dimensiones (co).

Las capas de agrupación y aplanado no tienen parámetros entrenables.

Las capas densas tienen una matriz entrenable \(W_l\) de dos dimensiones (m,p), siendo m el nº de carácteristicas de la salida de la capa (el vector \(X_l\)) y p el número de características de la entrada a la capa (el vector \(X_{l-1}\))

El proceso de retropropagación#

En cuadernos anteriores se ha justificado el proceso de retropropagación de las capas densas que se incluye en la maqueta. Aquí se va a justificar las fórmulas usadas a partir de un ejemplo teórico de dimensión reducida en las condiciones de la convolución expuestas. A continuación se muestra un gráfico del proceso de entrenamiento de un lote de 32 imágenes con la arquitectura LetNet5. En el se indican los pasos forward de cada una de las capas, el final de proceso donde se obtiene las probabilidades de clase con la función softmax y el cálculo de la función de pérdida a partir de la entropía cruzada (\(C\)).

En este proceso final se obtiene el grandiente del coste con respecto a la combinación lineal de la última capa (\(\frac{\partial C}{\partial Z ^L}\)), este gradiente que en el gráfico y en las rutinas programadas utiliza la nomeclatura dA comparte la dimensión con los tensores Z y A de cada capa. El primer proceso de retropropagación (BAC1 en el esquema) arranca con dA8 que es el gradiente de coste de la capa 8. Hay que entender Softmax como una activación específica. Por eso la entrada a esta función es Z8 la combinación lineal de la última capa. La salida de la función softmax para una observación x es un vector probabilidad p con la probabilidad de cada etiqueta. Para todo el lote es una matriz P donde cada fila es la probabilidad por observación. Más adelante comprobaremos que este gradiente de la capa final cuando se usa softmax unido a la función de coste de entropia cruzada resulta algo tan sintético como:

\[\frac{\partial C}{\partial Z ^L} = P - Y\]

Siendo \(P = softmax(Z^L)\) y \(Y\) una matriz one-hot de las etiquetas reales.

Por tanto los procesos de back-propagación siempre tienen la misma estructura:

Partiendo del gradiente de coste con respecto a la ponderación lineal de su capa (\(\frac{\partial C}{\partial Z ^l}\)), obtener o propagar el de la capa anterior (\(\frac{\partial C}{\partial Z ^{l-1}}\)).

\[\frac{\partial C}{\partial Z ^l} \rightarrow \frac{\partial C}{\partial Z ^{l-1}}\]

Obtiener el gradiente del coste con respecto a los pesos y bias de su capa, siempre y cuando sean capas entrenables:

\[\frac{\partial C}{\partial W ^l}; \frac{\partial C}{\partial B ^l}\]

Justificación de la retropropagación en convolución#

Para realizar esta justificación suponemos una única observación y un único canal (n = c = co = ci = 1).

Además para simplificar las fórmulas al máximo se toma en \(X_{n-1}\) h=b=4 en la entrada a la convolución y debido al filtro aplicado la salida se reduce en \(X_n\) a h=b=2 (por no usar relleno a ceros). Además el tamaño del filtro es f=3.

Dada una capa convolucional \(l\) cuya entrada suponemos definida por una matriz

\[\begin{split}\begin{bmatrix} x_{11} & x_{12} & x_{13} & x_{14} \\ x_{21} & x_{22} & x_{23} & x_{24} \\ x_{31} & x_{32} & x_{33} & x_{34} \\ x_{41} & x_{42} & x_{43} & x_{44} \\ \end{bmatrix} \end{split}\]

Esta matriz puede estar representando los datos de una observación de la capa de entrada a la red neuronal o la salida de la activación de la capa \(l-1\), que en su caso vendrá notada por \(A^{l-1}\).

En la capa \(l\) tenemos definida una convolución simple (suponemos un canal de entrada y uno de salida) que requiere una matriz de pesos o filtro \(W^l\) y una matriz de bias \(B^l\), suponemos un filtro 3x3 y dado que suponemos un sólo canal el bias es una matriz unidimensional:

\[\begin{split}W^l = \begin{bmatrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ w_{31} & w_{32} & w_{33} \\ \end{bmatrix} \end{split}\]

\[B^l = \begin{bmatrix} b \end{bmatrix} \]

Por comodidad sólo se usa superindice con el orden de la capa en las matrices, pero en los elementos de las matrices no se utiliza superíndice, si no sólo el subindice correspondiente. Así se nota la matriz \(W^l\) y sus elementos \(w_{ij}\) en lugar de \(w^l_{ij}\) por no complicar más la notación.

La matriz \(Z^l = W^l \otimes A^{l-1} \oplus B^l\), resultado de aplicar el filtro convolucional y sumar el bias, viene dada por:

\[\begin{split}\begin{bmatrix} x_{11} \cdot w_{11} + x_{12} \cdot w_{12}+x_{13} \cdot w_{13}+x_{21} \cdot w_{21}+x_{22} \cdot w_{22}+x_{23} \cdot w_{23}+x_{31} \cdot w_{31}+x_{32} \cdot w_{32}+x_{33} \cdot w_{33}+b & x_{12} \cdot w_{11} + x_{13} \cdot w_{12} + x_{14} \cdot w_{13} + x_{22} \cdot w_{21} + x_{23} \cdot w_{22} + x_{24} \cdot w_{23} + x_{32} \cdot w_{31} + x_{33} \cdot w_{32} + x_{34} \cdot w_{33} + b \\ x_{21} \cdot w_{11} + x_{22} \cdot w_{12} + x_{23} \cdot w_{13} + x_{31} \cdot w_{21} + x_{32} \cdot w_{22} + x_{33} \cdot w_{23} + x_{41} \cdot w_{31} + x_{42} \cdot w_{32} + x_{43} \cdot w_{33} + b & x_{22} \cdot w_{11} + x_{23} \cdot w_{12} + x_{24} \cdot w_{13} + x_{32} \cdot w_{21} + x_{33} \cdot w_{22} + x_{34} \cdot w_{23} + x_{42} \cdot w_{31} + x_{43} \cdot w_{32} + x_{44} \cdot w_{33} + b \end{bmatrix} \end{split}\]

Si se aplica la función de activación resulta \(A^l = f(Z^l) = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \)

En el proceso de retropropagación, al procesar la capa \(l+1\) se habrá retropropagado una matriz con el gradiente del coste con relación a la ponderación lineal \(Z^l\), con igual dimensión que \(Z^l\) y \(A^l\) y que se nota:

\[\begin{split}\frac{\partial C}{\partial Z^l} = \begin{bmatrix} \delta_{11} & \delta_{12} \\ \delta_{21} & \delta_{22} \end{bmatrix} = \begin{bmatrix} \frac{\partial C}{\partial z_{11}} & \frac{\partial C}{\partial z_{12}} \\ \frac{\partial C}{\partial z_{21}} & \frac{\partial C}{\partial z_{22}} \end{bmatrix} \end{split}\]

El objetivo del proceso de retropropagación de la capa \(l\) es obtener el gradiente del coste en relación a los pesos \(W^l\) y del bias \(B^l\), estos gradientes tiene igual dimensión que \(W^l\) y \(B^l\). Se observa en la notación que es una matriz jacobiana con las derivadas primeras del coste con respecto a cada peso:

\[\begin{split}\frac{\partial C}{\partial W^l} = \begin{bmatrix} \frac{\partial C}{\partial w_{11}} & \frac{\partial C}{\partial w_{12}} & \frac{\partial C}{\partial w_{13}} \\ \frac{\partial C}{\partial w_{21}} & \frac{\partial C}{\partial w_{22}} & \frac{\partial C}{\partial w_{23}} \\ \frac{\partial C}{\partial w_{31}} & \frac{\partial C}{\partial w_{32}} & \frac{\partial C}{\partial w_{33}} \\ \end{bmatrix} \end{split}\]

\[\frac{\partial C}{\partial B^l} = \begin{bmatrix} \frac{\partial C}{\partial b} \end{bmatrix} \]

Por la regla de la cadena, el término \( \frac{\partial C}{\partial w_{11}}\) se obtiene:

\[ \frac{\partial C}{\partial w_{11}} = \frac{\partial C}{\partial a_{11}} \frac{\partial a_{11}}{\partial w_{11}} + \frac{\partial C}{\partial a_{12}} \frac{\partial a_{12}}{\partial w_{11}} + \frac{\partial C}{\partial a_{21}} \frac{\partial a_{21}}{\partial w_{11}} + \frac{\partial C}{\partial a_{22}} \frac{\partial a_{22}}{\partial w_{11}} \]

Como \(\frac{\partial C}{\partial a_{ij}} = \delta_{ij}\), la matriz \(\frac{\partial C}{\partial W^l}\), dónde el resultado anterior aparece en el término 1,1 es:

\[\begin{split}\begin{bmatrix} \delta_{11} \cdot x_{11} + \delta_{12} \cdot x_{12} + \delta_{21} \cdot x_{21} + \delta_{22} \cdot x_{22} & \delta_{11} \cdot x_{12} + \delta_{12} \cdot x_{13} + \delta_{21} \cdot x_{22} + \delta_{22} \cdot x_{23} & \delta_{11} \cdot x_{13} + \delta_{12} \cdot x_{14} + \delta_{21} \cdot x_{23} + \delta_{22} \cdot x_{24} \\ \delta_{11} \cdot x_{21} + \delta_{12} \cdot x_{22} + \delta_{21} \cdot x_{31} + \delta_{22} \cdot x_{32} & \delta_{11} \cdot x_{22} + \delta_{12} \cdot x_{23} + \delta_{21} \cdot x_{32} + \delta_{22} \cdot x_{33} & \delta_{11} \cdot x_{23} + \delta_{12} \cdot x_{24} + \delta_{21} \cdot x_{33} + \delta_{22} \cdot x_{34} \\ \delta_{11} \cdot x_{31} + \delta_{12} \cdot x_{32} + \delta_{21} \cdot x_{41} + \delta_{22} \cdot x_{42} & \delta_{11} \cdot x_{32} + \delta_{12} \cdot x_{33} + \delta_{21} \cdot x_{42} + \delta_{22} \cdot x_{43} & \delta_{11} \cdot x_{33} + \delta_{12} \cdot x_{34} + \delta_{21} \cdot x_{43} + \delta_{22} \cdot x_{44} \end{bmatrix} \end{split}\]

El gradiente del coste con respecto a \(B^l\), usando la regla de la cadena resulta:

\[ \frac{\partial C}{\partial b} = \frac{\partial C}{\partial z_{11}} \frac{\partial z_{11}}{\partial b} + \frac{\partial C}{\partial z_{12}} \frac{\partial z_{12}}{\partial b} + \frac{\partial C}{\partial z_{21}} \frac{\partial z_{21}}{\partial b} + \frac{\partial C}{\partial z_{22}} \frac{\partial z_{22}}{\partial b} \]

Y como \(\frac{\partial a_{ij}}{\partial b} = 1\) se tiene:

\[ \frac{\partial C}{\partial B^l} = \delta_{11} + \delta_{12} + \delta_{21} + \delta_{22} \]

Se puede observar que la matriz \(\frac{\partial C}{\partial W^l}\) se construye recorriendo uno a uno los elementos de \(\frac{\partial C}{\partial Z^l}\) a la vez que nos movemos usando las dimensiones del filtro \(W^l\) sobre la matriz \(A^{l-1}\) y los subproductos escalares entre \(\delta_{ij}\) y las submatrices (3x3) se van acumulando en \(\frac{\partial C}{\partial W^l}\). El primer subproducto se ve en la siguiente imagen:

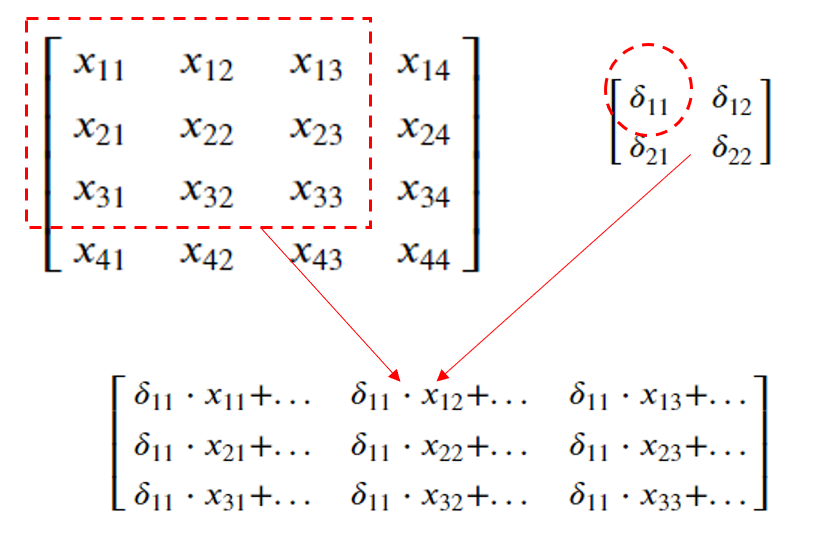
Y el siguiente subproducto sería:

El código programado aparece en la función backward de la clase conv2DLayer (ajustando la notación):

             dW[co, :] += Aprev[i, :, _h:_h+f, _b:_b+f] * Delta[i, co, _h,_b]

La última operación del proceso de retropropagación de la capa \(l\) consiste en obtener la matriz jacobiana

\[ \frac{\partial C}{\partial Z^{l-1}} \]

Que es de la misma dimensión que \(A^{l-1}\), en este ejemplo (4x4), siendo el elemento \((i,j)\) el resultado de obtener

\[ \frac{\partial C}{\partial x_{ij}} \]

Por la regla de la cadena, el término \( \frac{\partial C}{\partial x_{11}}\) se obtiene:

\[ \frac{\partial C}{\partial x_{11}} = \frac{\partial C}{\partial z_{11}} \frac{\partial z_{11}}{\partial x_{11}} + \frac{\partial C}{\partial z_{12}} \frac{\partial z_{12}}{\partial x_{11}} + \frac{\partial C}{\partial z_{21}} \frac{\partial z_{21}}{\partial x_{11}} + \frac{\partial C}{\partial z_{22}} \frac{\partial z_{22}}{\partial x_{11}} = \delta_{11} \cdot w_{11} \]

La matriz jacobiana completa

\[\begin{split}\frac{\partial C}{\partial Z^{l-1}} = \begin{bmatrix} \frac{\partial C}{\partial x_{11}} & \frac{\partial C}{\partial x_{12}} & \frac{\partial C}{\partial x_{13}} & \frac{\partial C}{\partial x_{14}}\\ \frac{\partial C}{\partial x_{21}} & \frac{\partial C}{\partial x_{22}} & \frac{\partial C}{\partial x_{23}} & \frac{\partial C}{\partial x_{24}} \\ \frac{\partial C}{\partial x_{31}} & \frac{\partial C}{\partial x_{32}} & \frac{\partial C}{\partial x_{33}} & \frac{\partial C}{\partial x_{34}}\\ \frac{\partial C}{\partial x_{41}} & \frac{\partial C}{\partial x_{42}} & \frac{\partial C}{\partial x_{43}} & \frac{\partial C}{\partial x_{44}}\\ \end{bmatrix} \end{split}\]

Entonces \(\frac{\partial C}{\partial Z^{l-1}}\) resulta:

\[\begin{split}\begin{bmatrix} w_{11} \cdot \delta_{11} & w_{12} \cdot \delta_{11} + w_{11} \cdot \delta_{12} & w_{13} \cdot \delta_{11} + w_{12} \cdot \delta_{12} & w_{13} \cdot \delta_{12} \\ w_{21} \cdot \delta_{11} + w_{11} \cdot \delta_{21} & w_{22} \cdot \delta_{11} + w_{21} \cdot \delta_{12} + w_{12} \cdot \delta_{21} + w_{11} \cdot \delta_{22} & w_{23} \cdot \delta_{11} + w_{22} \cdot \delta_{12} + w_{13} \cdot \delta_{21} + w_{12} \cdot \delta_{22} & w_{23} \cdot \delta_{12} + w_{13} \cdot \delta_{22} \\ w_{31} \cdot \delta_{11} + w_{21} \cdot \delta_{22} & w_{32} \cdot \delta_{11} + w_{31} \cdot \delta_{12} + w_{22} \cdot \delta_{21} + w_{21} \cdot \delta_{22} & w_{33} \cdot \delta_{11} + w_{32} \cdot \delta_{12} + w_{23} \cdot \delta_{21} + w_{22} \cdot \delta_{22} & w_{33} \cdot \delta_{12} + w_{23} \cdot \delta_{22} \\ w_{31} \cdot \delta_{21} & w_{32} \cdot \delta_{21} + w_{31} \cdot \delta_{22} & w_{33} \cdot \delta_{21} + w_{32} \cdot \delta_{22} & w_{33} \cdot \delta_{22} \end{bmatrix} \end{split}\]

La forma de obtener esta matriz es acumulando el producto escalar

\[ \delta_{ij} \cdot W^l \]

En la matriz \(\frac{\partial C}{\partial Z^{l-1}}\) cuya dimensión coindicen con \(A^{l-1}\), en este ejemplo 4x4, acumulando el resultado matricial, en este caso 3x3, en la submatriz de acuerdo al movimiento del filtro. El primer subproducto escalar se ve en la siguiente imagen:

Y el siguiente subproducto en:

El código programado aparece en la función backward de la clase conv2DLayer (ajustando la notación):

             DeltaPrev[i, :, _h:_h+f, _b:_b+f] += self.W[co, :] * Delta[i, co, _h,_b]

El código anterior finaliza concatenado el producto de Hadamard de la derivada primera de la función de activación en \(Z^{l-1}\)

Softmax y cross-entropy#

A la salida de la última capa se aplica la función softmax. Si el vector \(z\) tiene la transformación lineal de la última capa (antes de aplicar la función de activación) la probabilidad de la neurona \(j\) de salida es de acuerdo a la función softmax:

\[p_j = \frac{e^{z_j}}{\sum_j{e^{z_j}}}\]

Finalmente la pérdida se obtiene con la función entropia cruzada que es:

\[- \sum_j {y_j \cdot ln(p_j)}\]

Dónde \(y_j\) es el valor de la etiqueta en formato one-hot (vector con tantos dígitos como posibles etiquetas hay y que lleva todo ceros y un 1 en la posición que corresponde a la etiqueta).

El uso de softmax y cross-entropy a la salida de la última capa (\(L\)) como se indica hace que el gradiente del coste con respecto a la transformación lineal de esa última capa:

\[ \frac{\partial C}{\partial z^l_i} = p_i - y_i\]

Para comprobarlo en un caso sencillo, se supone que una observación que tiene una transformación lineal:

\[z=(z_1, z_2, z_3)\]

Sabiendo que las etiquetas reales de esa observación en formato one-hot viene dado por

\[y=(y_1, y_2, y_3)\]

La probabilidad usando la función softmax es:

\[p=(p_1, p_2, p_3)\]

\[p_1 = \frac{e^{z_1}}{e^{z_1} + e^{z_2} + e^{z_3}}\]

\[p_2 = \frac{e^{z_2}}{e^{z_1} + e^{z_2} + e^{z_3}}\]

\[p_3 = \frac{e^{z_3}}{e^{z_1} + e^{z_2} + e^{z_3}}\]

La función de coste por entropia cruzada es:

\[ C = -y1 \cdot ln(p_1) -y2 \cdot ln(p_2) -y3 \cdot ln(p_3) \]

El gradiente del coste con respecto a \(z\) será el vector

\[\begin{pmatrix} \frac{\partial C}{\partial z_1}, \frac{\partial C}{\partial z_2}, \frac{\partial C}{\partial z_3} \end{pmatrix}\]

Desarrollando la primera componente:

\[\frac{\partial C}{\partial z_1} = -y1 \frac{1}{p_1}\frac{\partial p_1}{\partial z_1} -y2 \frac{1}{p_2}\frac{\partial p_2}{\partial z_1} -y3 \frac{1}{p_3}\frac{\partial p_3}{\partial z_1}\]

Quedando:

\[\frac{\partial C}{\partial z_1} = \frac{-y_1e^{z_2}-y_1e^{z_3}+y_2e^{z_1}+y_3e^{z_1}}{e^{z_1} + e^{z_2} + e^{z_3}}\]

Sumando y restando el término \(y_1e^{z_1}\) la fracción se puede poner

\[\frac{\partial C}{\partial z_1} = \frac{-y_1 (e^{z_1} + e^{z_2} + e^{z_3}) + e^{z_1}(y_1+y_2+y_3)}{e^{z_1} + e^{z_2} + e^{z_3}}\]

Pero como el vector \(y\) es un formato one-hot, se cumple que \(y_1+y_2+y_3=1\) quedado la expresión:

\[\frac{\partial C}{\partial z_1} = -y_1 + \frac{e^{z_1}}{e^{z_1} + e^{z_2} + e^{z_3}} = p_1 - y_1\]

Haciendo lo mismo con las otras 2 derivadas parciales se ve que el vector gradiente se obtiene así:

\[\begin{pmatrix} \frac{\partial C}{\partial z_1}, \frac{\partial C}{\partial z_2}, \frac{\partial C}{\partial z_3} \end{pmatrix} = \begin{pmatrix}p_1 - y_1, & p_2 - y_2, & p_3 - y_3 \end{pmatrix} = p - y\]

Este gradiente es el que aparece en el esquema anterior de LetNet5 identificado como dA8, una matriz de 32 filas y 10 columnas para cada una de las 10 posibles etiquetas. Esta matriz jacobiana es la que arranca el proceso de retro-propagación de los gradientes del coste.

Optimización ADAM#

Al actualizar los pesos y bias con sus gradientes de coste multiplicados por la tasa de entrenamiento (\(\eta\)) en arquitecturas que mezclan capas de diferentes naturaleza surge el inconveniente de que las velocidades de crecimiento de los gradientes no son homogéneas y sería preciso utilizar valores de \(\eta\) diferentes en cada capa.

Como sería muy difícil estimar estos valores en cada capa, hay algoritmos, por ejemplo Root Mean Square Propagation (RMSprop) que utilizan una media móvil que promedia más los valores actuales que los antiguos. A la vez se utiliza un momento de segundo orden para normalizar los elementos del gradiente (pues la raiz cuadrada de de la estimación del momento del segundo orden equivale a la desviación estándar).

ADAM (o estimación adaptativa del momento) añade a RMSprop el cálculo de un momento y es el método más utilizado. Su fórmula es:

\[m_{t+1}=\beta \cdot m_t + (1 - \beta) \bigtriangledown f_i(w_t)\]

\[v_{t+1}=\alpha \cdot v_t + (1 - \alpha) \bigtriangledown f_i(w_t) ^2\]

\[w_{t+1} = w_t - \eta \frac{m_t}{\sqrt{v_t + 1} + \epsilon}\]

Donde \(\epsilon\) es un valor muy próximo a cero (\(10^{-7}\) por ejemplo) para evitar divisiones por cero