Funciones#
Una función \(f:A\subset{\mathbb R}\to {\mathbb R}\) es una regla que asigna a cada elemento de \(A\) un único elemento en \({\mathbb R}\).
El dominio de la función es el conjunto \(A\) donde \(f\) tiene sentido.
La imagen (o rango) son todos los puntos de \({\mathbb R}\) que proceden de algún \(x\) en \(A\). Se designa mediante \(f(A)\).
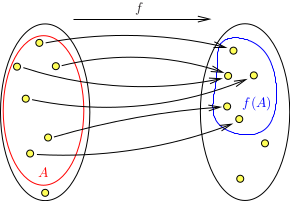
Fig. 1 Diagrama de flechas de una función con su dominio \(A\) y su imagen \(f(A)\)#
Ejemplos#
De millas náuticas, \(x\), a km., \(f(x)\)
Dominio \(\{x\ge 0\}\)
De grados Farenheit, \(x\), a grados Celsius, \(f(x)\)
Dominio \(\{x\ge -459,67\}\)
Crecimiento bacteriano:
con \(N_0 = \) población inicial de individuos, \(a =\) ritmo de crecimiento.
Volumen de la esfera de radio \(x\), $\( V(x)=\dfrac{4\pi}{3}x^3 \)$
Deflexión de una viga en voladizo con peso uniforme \(\omega\), longitud \(L\), módulo de elasticidad \(E\) y momento de inercia \(I\): $\( f(x)=-\dfrac{w}{24EI}(x^4-4Lx^3+6L^2x^2) \)$
Valor de capital inicial de \(10\) (en miles de euros) en una cuenta con interés del 4% en \(t\) años,
Magnitud de la escala Richter de un terremoto (\(x=\) energía del terremoto en julios)
Atención
No es función
pues para cada \(x\) hay dos posibilidades de \(y\).
Dominio y rango#
\(f(x)\) |
Dominio |
Rango |
|---|---|---|
\(x^2\) |
\(\mathbb{R}\) |
\(\{y:y\geq 0\}\) |
\(\cos(x)\) |
\(\mathbb{R}\) |
\(\{y:-1\leq y \leq 1\}\) |
\(\frac{1}{x+1}\) |
\(\{x:x\neq -1\}\) |
\(\{y:y\neq 0\}\) |
Gráfica de una función#
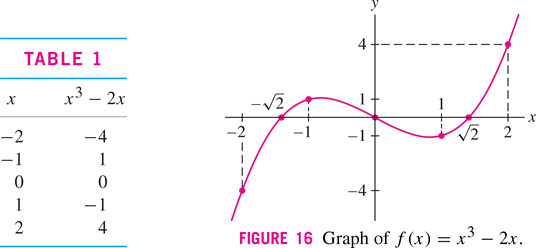
Fig. 2 Rogawski Calculus, Second Edition Copyright © 2012 W. H. Freeman and Company#
Raíces o ceros de una función#

Fig. 3 Rogawski Calculus, Second Edition Copyright © 2012 W. H. Freeman and Company#
Test de línea vertical#
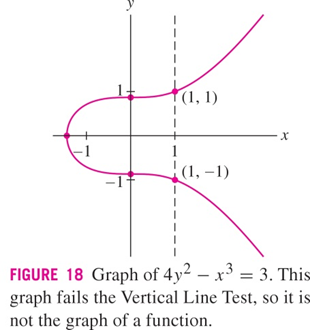
Fig. 4 Rogawski Calculus, Second Edition Copyright © 2012 W. H. Freeman and Company#
