Algunas parametrizaciones

Recta

La recta que pasa por el punto \(A\in\mathbb{R}^n\) y tiene como vector director \(\mathbf{v}\) se puede parametrizar de la siguiente manera

\[ \mathbf{c}(t)=A+t\mathbf{v},\qquad t\in \mathbb{R} \]

En \(\mathbb{R}^2\), si \(A=(x_0,y_0)\) y \(\mathbf{v}=(v_1,v_2)\), obtenemos $\( x(t)=x_0+tv_1,\quad y(t)=y_0+tv_1,\quad t\in\mathbb{R} \)$

Note

Ambas coordenadas son función del parámetro \(t\); despejándolo e igualando obtendremos la ecuación de la recta

Segmento

El segmento que une los puntos \(A\) y \(B\) de \(\mathbb{R}^n\) se puede parametrizar de la siguiente manera

\[ \mathbf{c}(t)=A+t(B-A),\quad t\in[0,1] \]

Ejercicio

Parametrizar el segmento que une \(A=(1,2,0)\) y \(B=(2,1,2)\)

Note

El punto medio del segmento es \(\mathbf{c}(1/2)\)

Circunferencia

La circunferencia unidad

\[ C:\, x^2+y^2=1 \]

se parametriza mediante

\[ x(t)=\cos t,\quad y(t)=\sin t,\qquad t\in[0,2\pi) \]

En general, una circunferencia centrada en \((x_0,y_0)\) de radio \(r\) se puede parametrizar haciendo

\[ x(t)=x_0+r\cos t,\quad y(t)=y_0+r\sin t,\qquad t\in[0,2\pi) \]

Ejercicio

Dar una ecuación implı́cita y una parametrización de la circunferencia centrada en (0, 2) de radio 4. La parametrización ha de tener orientación antihoraria y que en tiempo 0 pase por el punto (4, 2).

Elipse

Dada la elipse

\[ E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \]

observamos que un punto \((x,y)\in E\) cumple que \(\left(\frac{x}{a},\frac{y}{b}\right)\in C\), siendo \(C\) la circunferencia unidad. Por tanto

\[ \frac{x}{a}=\cos t,\quad \frac{y}{b}=\sin t,\qquad t\in[0,2\pi) \]

Despejando obtenemos la parametrización de la elipse

\[ \mathbf{c}(t)=(a\cos t,b\sin t),\quad t\in[0,2\pi) \]

En general, una elipse centrada en \((x_0,y_0)\) de semiejes \(a\) y \(b\) se puede parametrizar haciendo

\[ x(t)=x_0+a\cos t,\quad y(t)=y_0+b\sin t,\qquad t\in[0,2\pi) \]

Hipérbola

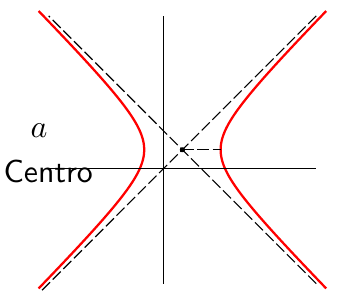
La hipérbola \(H: x^2-y^2=1\) tiene dos ramas. Parametrizamos primero la rama derecha, que podemos describir con la ecuación \(x=\sqrt{y^2+1}\)

Sabemos que la función \(y=\sinh t\) es una función real biyectiva: dado \(y\in\mathbb{R}\), existe un único \(t\in\mathbb{R}\) ta que \(y=\sinh t\).

Note

Recuerda la identidad \(\cosh^2 t-\sinh^2t =1\)

Usando el cambio de variable \(y=\sinh t\) tenemos

\[ x=\sqrt{1+\sinh^2 t}=\cosh t \]

Por tanto, una parametrización de la rama derecha de la hipérbola \(H\) es

\[ \mathbf{c}(t)=(\cosh t,\sinh t),\quad t \in\mathbb{R} \]

La otra rama se parametriza de la misma manera, pero \(x(t)\) tiene signo opuesto.

En general, la hipérbola centrada en \((x_0,y_0)\) de semiejes \(a\) y \(b\) dada por la ecuación

\[ \frac{(x-x_0)^2}{a^2}-\frac{(y-y_0)^2}{b^2}=1 \]

se puede parametrizar a través de las siguiente funciones

• Rama positiva:

\[ \mathbf{c}_1(t)=(x_0+a\cosh t,y_0+b\sinh t),\quad t \in\mathbb{R} \]

• Rama negativa:

\[ \mathbf{c}_2(t)=(x_0-a\cosh t,y_0+b\sinh t),\quad t \in\mathbb{R} \]

Ejercicios

• Representar gráficamente y encontrar una parametrización de las curvas

  • \(x^2=8(2-y)\)

  • \(\frac{(y-4)^2}{36}-x^2=1\)