El Logaritmo#
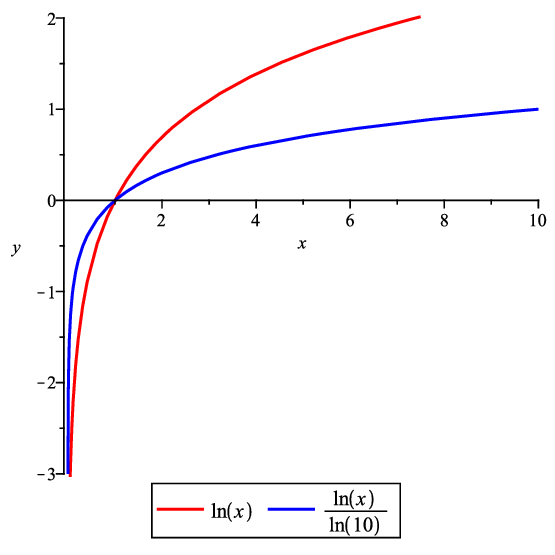
Comparación bases#
Comparaci’on de logaritmos con base \(e\) y base \(10\)
Propiedades#
- \[ \log_{b}x=n \Leftrightarrow x=b^n \]
- \[ \log_{a}a^x = x\qquad a^{\log_a x}=x \]
- \[ \log_b(x)=\frac{\log_k x}{\log_k b}\quad \text{Cambio de base} \]
- \[ \log_b(xy)=\log_b(x)+\log_b(y) \]
- \[\log_b(x^y)=y\log_b(x) \]
Cambio de base#
El cambio de base del logaritmo
\[
\log_b(x)=\frac{\log_k x}{\log_k b}
\]
se prueba teniendo en cuenta que si \(y=\log_b x\) entonces \(b^y=x\). Tomando logaritmos en la segunda identidad:
\[
\log_k(b^y)=\log_k x\Rightarrow y\log_k(b)=\log_k x
\]
Sustituyendo llegamos a la identidad del cambio de base.
Derivada#
\[
e^y=x\Leftrightarrow y=\ln x
\]
\[
\frac{d}{dx}\left[
e^y=x
\right]\rightarrow y'e^y=1\Leftrightarrow y'=\frac{1}{e^y}=e^{-y}=\frac{1}{x}
\]
Como el dominio del logaritmo es \(x>0\), entonces \(y'>0\) y la función logaritmo es creciente.
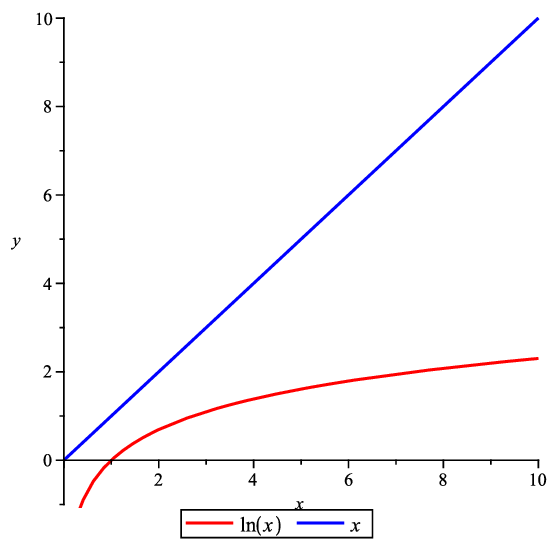
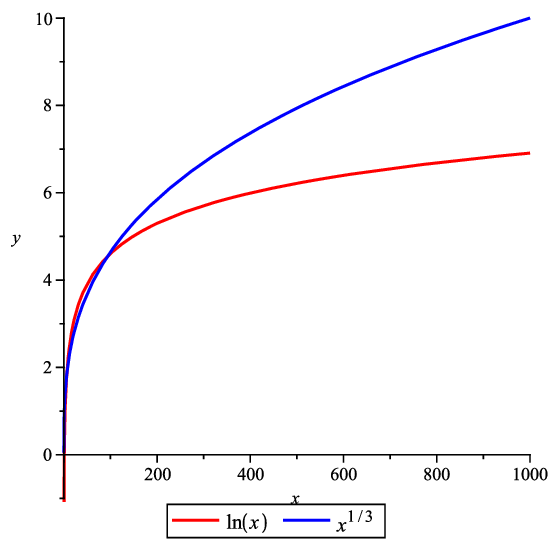
Comparación con potencias#
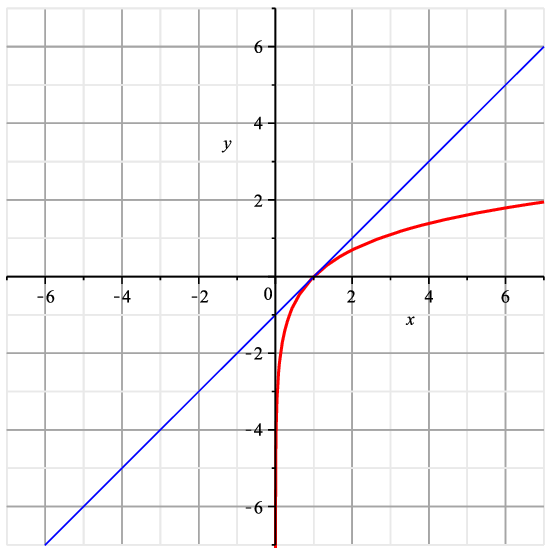
Cerca de \(x=1\)#
Inversa: la exponencial#
Gr’afica de \({\color{red}f(x)=e^x}\) y de \({\color{blue}f^{-1}(x)=\log x}\)