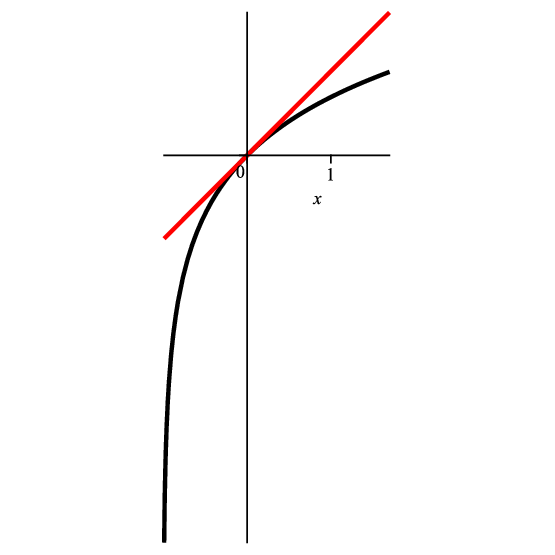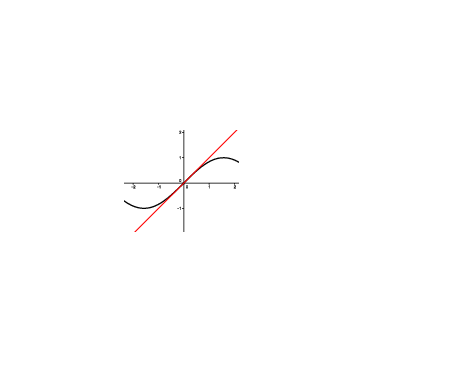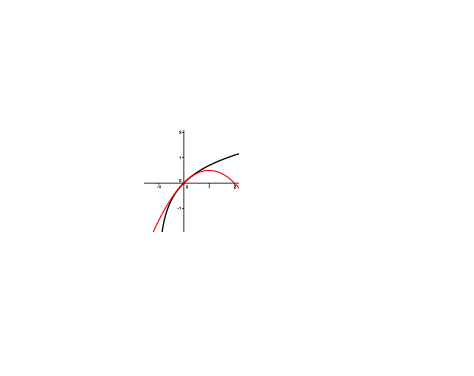Aproximaciones usando las derivadas

Motivación

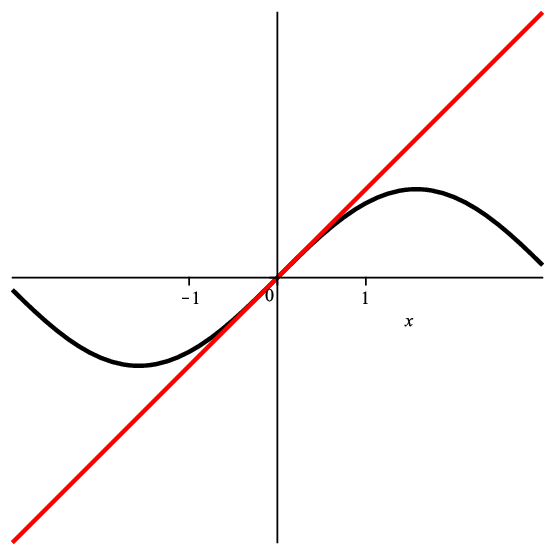
Aunque \(\sin x\) y \(\log (1+x)\) tengan la misma aproximación lineal en \(x=0\), sus gráficas son muy diferentes:

\[ \sin x \approx x,\quad x\to 0\qquad \log(1+x)\approx x,\quad x\to 0. \]

Seno

Logaritmo

Cerca de \(0\), \(\sin x\) y \(\log(1+x)\) son funciones que se parecen bastante (tienen la misma aproximación lineal) pero veremos que otras aproximaciones mejores que la lineal captan las diferencias entre ambas gráficas.

Recordatorio: la recta tangente

Note

Sea \(f\) continua y derivable en un intervalo que incluye \(x=a\). La recta tangente a \(f\) en \(a\),

\[ l(x)=f(a)+f'(a)(x-a), \]

es la única función lineal que cumple

\[ l(a)=f(a),\quad l'(a)=f'(a). \]

Vamos a generalizar la noción de aproximación lineal a aproximaciones polin’omicas de otros grados usando esta observación. Estas aproximaciones serán los polinomios de Taylor.

Polinomio de Taylor

Queremos aproximar una función \(f(x)\) en un punto \(x=a\).

Sea \(f:[a,b]\to\mathbb{R}\) tal que existen las derivadas hasta el orden \(n+1\).

Definition 1

El polinomio de Taylor de \(f\) de orden \(n\) en el punto \(x=a\), \(P_{n,a}^f(x)\), es el único polinomio que satisface que \(P_{n,a}^f(a)=f(a)\) y además todas sus derivadas hasta orden \(n\) en \(x=a\) coinciden con las de \(f\), es decir:

\[ (P_{n,a}^f)^{(i}(a)=f^{(i}(a), \quad i=0,\ldots,n \]

es decir

\[ P_{n,a}^f(a)=f(a),\quad (P_{n,a}^f)'(a)=f'(a),\quad (P_{n,a}^f)''(a)=f''(a),\cdots,(P_{n,a}^f)^{(n}(a)=f^{(n}(a) \]

Expresión analítica

El polinomio de Taylor de \(f\) de orden \(n\) en el punto \(x=a\) es

\[ P_{n,a}^f(x)=\displaystyle\sum_{i=0}^n\frac{f^{(i}(a)}{i!}(x-a)^i \]

con la convención \(0!=1\) y \(f^{(i}=f\); de este modo, el polinomio es:

\[ P_{n,a}^f(x)=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\cdots+\frac{f^{(n}(a)}{n!}(x-a)^n \]

Note

El polinomio de Taylor de orden \(1\) en \(a\), es la aproximación lineal de \(f\) en \(a\)

\[ P^f_{a,1}(x)=f(a)+f'(a)(x-a). \]

Polinomio de McLaurin

En el caso que \(a=0\), tenemos una aproximación centrada en el origen que es el polinomio de McLaurin

\[ f(x)=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\cdots+\frac{f^{(n}(0)}{n!}x^n+\frac{f^{(n+1}(r)}{(n+1)!}x^{n+1} \]

• El polinomio de Maclaurin de una función par solamente tiene potencias pares.

• El polinomio de Maclaurin de una función impar solamente tiene potencias impares.

Comparación con el polinomio de McLaurin de orden 2

Aunque las aproximaciones lineales en \(a=0\) de \(\sin x\) y \(\log(1+x)\) eran la misma, las aproximaciones de orden dos, ya distinguen mejor entre el comportamiento de ambas cerca de \(a=0\).

Seno

Logaritmo

\[ \sin x\approx x,\quad x\to 0. \qquad \log(1+x)\approx x-\frac{x^2}{2},\quad x\to 0. \]

Ejemplos

Enlace

Teorema de Taylor

Los polinomios de Taylor aproximan mejor a la función cerca de \(a\) a medida que su orden aumenta.

Theorem 8

Sea \(f\) una función con \(n\) derivadas continuas en \(a\) (es decir, \(f\) de clase \(C^n\) cerca de \(a\)). Entonces

\[ f(x)=f(a)+f'(a)(x-a)+\dfrac{f''(a)}{2!}(x-a)^2+\cdots+\dfrac{f^{\left.n\right)}(a)}{n!}(x-a)^n+o((x-a)^n) \]

En otras palabras el error cometido al sustituir \(f(x)\) por su polinomio de Taylor de orden \(n\) es más pequeño que \((x-a)^n\) cuando \(x\) está suficientemente cerca de \(a\) y por tanto el polinomio de Taylor es una buena aproximación de \(f\) cerca de \(a\).

Aproximaciones de McLaurin de funciones elementales

\[ e^x=1+x+\frac{x^2}{2!}+\cdots+\frac{x^n}{n!}+\mathcal{o}(x^n),\quad x\to 0 \]

\[ \ln(1+x)=x-\frac{x^2}{2!}+\frac{x^3}{3!}-\cdots+(-1)^{n-1}\frac{x^n}{n!}+\mathcal{o}(x^{n}),\quad x\to 0 \]

\[ \sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots+(-1)^{n-1}\frac{x^{2n-1}}{(2n-1)!}+\mathcal{o}(x^{2n+2}),\quad x\to 0 \]

\[ \cos(x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots+(-1)^n\frac{x^{2n}}{(2n)!}+\mathcal{o}(x^{2n+1}),\quad x\to 0 \]