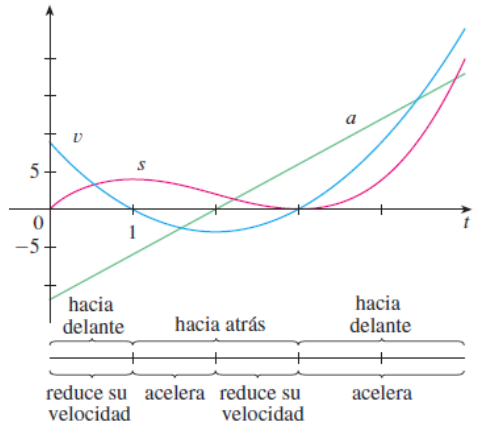
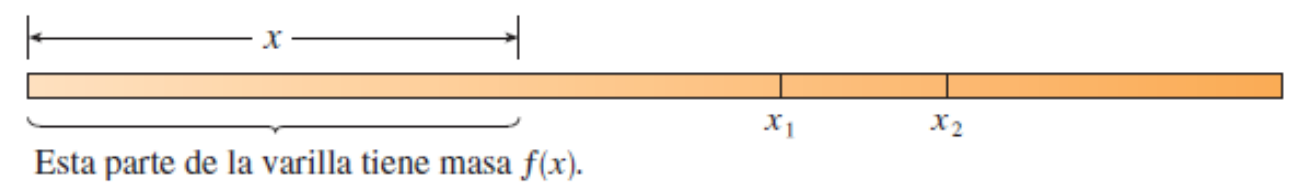Aplicaciones de la derivada#

Rapidez de cambio en ciencias naturales y sociales#

Movimiento de una partícula#

Si la posición de una partícula es \(s=f(t)=t^3-6t^2+9t\), la velocidad es igual a \(v(t)=\frac{ds}{dt}=3t^2-12t\) y la aceleración es \(a(t)=\frac{d^2s}{dt^2}=6t-12\).

fishy

Densidad Lineal#

Si una varilla o alambre tiene una masa que es función del punto de la varía, \(m(x)\), siendo \(x\) el punto, entonces la densidad será \(\rho(x)=\frac{dm}{dx}\).

fishy

Intensidad de una corriente#

La carga eléctrica de una corriente varía con el tiempo \(Q=Q(t)\), entonces la intesidad de la corriente (velocidad instantánea) del paso de los electrones es \(I=\frac{dQ(t)}{dt}\).

Problemas de modelización#

  • Se bombea aire en el interior de un globo esférico, de modo que su volumen aumenta a razón de 100 cm\(^3\)/s. ¿Con qué rapidez crece el radio del globo cuando el diámetro es exactamente 50 cm? La esfera de radio \(r\) tiene volumen

\[ V=\frac{4}{3}\pi r^3. \]

  • Un tanque de agua tiene forma de cono invertido. Su base tiene un raio de 2 m y su altura es de 4 m. Si se bombea en su interior agua a razón de 2 m\(^3\)/min, encuentre la razón a la cual sube el nivel del agua cuando ésta tiene una profundida de 3 m. El volumen del cono de altura \(h\) y base de radio \(r\) es:

\[ V=\frac{1}{3}\pi h r^2. \]

  • Se está inflando un globo esférico. Encuentre la razón de aumento del área superficial con respecto al radio \(r\) cuando \(r\)

    • 1 pie

    • 2 pies

    • 3 pies El area superficial de una esfera de radio \(r\) es \(S=4\pi r^2\). ¿Qué conclusión puede hacerse?

Ejercicio#

Se arrastra un pequeño peso con una cuerda de longitud \(a\) y de extremos \(P\) y \(Q\). El peso está atado al extremo \(P\) mientras que \(Q\) se mueve siempre en el mismo sentido a lo largo de una recta perpendicular a la posición original de \(PQ\). Demostrar que, si se escogen los ejes coordenados de manera que \(Oy\) es la recta fija por la que se mueve \(Q\) y \(Ox\) es la dirección original en la que la cuerda descansa, entonces la curva \(y(x)\) trazada por el peso verifica la ecuación

\[ \frac{dy}{dx}=-\frac{\sqrt{a^2-x^2}}{x} \]

Solución: la pendiente de la recta tangente a la curva \(y(x)\) en el punto \(x_0\) es

\[ -\frac{\sqrt{a^2-x_0^2}}{x_0} \]

y esa pendiente es la derivada de la función en \(x_0\). Por tanto

\[ \frac{dy}{dx}(x0)=-\frac{\sqrt{a^2-x_0^2}}{x_0}\Rightarrow \frac{dy}{dx}=-\frac{\sqrt{a^2-x^2}}{x} \]
fishy
fishy