Algunas series#

Serie geométrica#

La serie geométrica tiene una estructura \(a+ar+ar^2+\cdots+ar^{n-1}+\cdots = \sum_{n=1}^\infty ar^{n-1}\) con \(a\neq 0\)

Cada término se puede obtener del precedente multiplicando por \(r\).

Suma:

Si tomamos

\[\begin{align*} S_n&=a+ar+ar^2+\cdots+ar^{n-1}\\ rS_n&=ar+ar^2+\cdots+ar^{n} \end{align*}\]

Entonces

\[ S_n-rS_n = a-ar^n\Rightarrow S_n(1-r)=a-ar^n\Rightarrow S_n=\frac{a-ar^n}{1-r} \]

Tomando límites

\[ S=\lim_{n\to\infty} S_n = \lim_{n\to\infty}\frac{a-ar^n}{1-r}=\frac{a}{1-r}-\frac{a}{1-r}\lim_{n\to\infty}r^n =\frac{a}{1-r} \]

  • Si \(|r|<1\) entonces la serie converge al valor anterior

  • Si \(r\leq -1\) ó \(r>1\) la sicesión \(r^n\) es divergente y no existe la suma de la serie geométrica

Serie armónica#

La estructura de esta serie es:

\[ \sum_{n=1}^\infty \frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\ldots \]

Las sumas parciales:

\[\begin{align*} S_2&=1+\frac{1}{2}\\ S_4&=1+\frac{1}{2}+\left(\frac{1}{3}+\frac{1}{4}\right)\\ &>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)\\ &=1+\frac{1}{2}+\frac{1}{2}=1+\frac{2}{2}\\ S_8&=1+\frac{1}{2}+\left(\frac{1}{3}+\frac{1}{4}\right)+\left(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\right)\\ &>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\right)\\ &=1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=1+\frac{3}{2}\\ S_{16}&=1+\frac{1}{2}+\left(\frac{1}{3}+\frac{1}{4}\right)+\left(\frac{1}{5}+\cdots+\frac{1}{8}\right) +\left( \frac{1}{9}+\cdots+\frac{1}{16} \right)\\ &>1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=1+\frac{4}{2} \end{align*}\]

Del mismo modo \(S_{32}>1+\frac{5}{2}\) y \(S_{64}>1+\frac{6}{2}\).

En general

\[ S_{2^n}>1+\frac{n}{2} \]

por lo que, cuando \(n\to\infty\) se tiene \(S_{2^n}\to\infty\). La serie armónica es divergente.

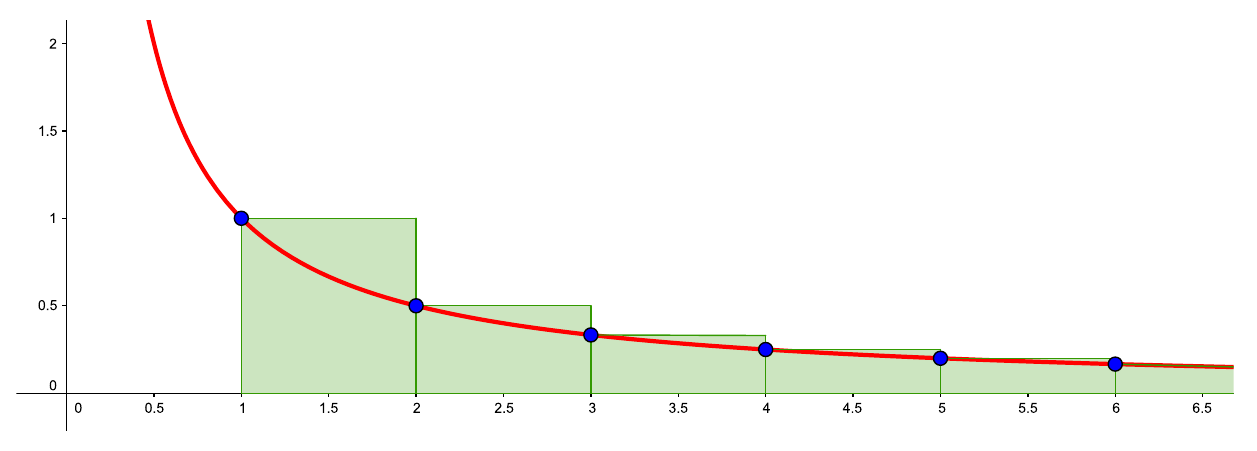
fishy

Podemos comprobar la divergencia a través de la comparación con la integral

\[ S=\sum_{n=1}^{\infty}\frac{1}{n},\qquad S_N=\sum_{n=1}^{N}\frac{1}{n} \]

Usando la gráfica vemos que

\[ S_N=\sum_{n=1}^{N}\frac{1}{n}\geq \int_1^{N+1}\frac{1}{x}dx=\log(N+1) \]

Por tanto

\[ S=\sum_{n=1}^{\infty}\frac{1}{n}\geq \lim_{N\to\infty}\int_1^{N+1}\frac{1}{x}dx=\lim_{N\to\infty}\log(N+1)=\infty \]

La serie armónica diverge.

La \(p\)-serie#

Dada la serie

\[ \sum_{n=1}^{\infty}\frac{1}{n^p} \]

veremos para qué valores de \(p\) la serie converge o diverge.

  • Si \(p<0\) se cumple que \(\lim_{n\to\infty} a_n = \lim_{n\to\infty}\left(\frac{1}{n^p}\right)=\infty\) y la serie diverge

  • Si \(p=0\) se cumple que \(\lim_{n\to\infty} \left(\frac{1}{n^p}\right)=1\neq 0\) y la serie diverge

  • Si \(p=1\) es la serie armónica y diverge

  • Si \(p>1\) vamos a aplicar la prueba de la integral:

Como \(f(x)=\frac{1}{x^p}\) es continua, positiva y decreciente (efectivamente \(f'(x)=-\frac{p}{x^{p+1}}<0\) en \([1,\infty)\)), entonces podemos aplicar la prueba de la integral:

\[\begin{align*} \int_1^\infty\frac{dx}{x^p}&=\lim_{t\to\infty}\int_1^t\frac{dx}{x^p}\\ &=\lim_{t\to\infty}\left[\frac{-1}{(p-1)x^{p-1}}\right]_1^t\\ &=\lim_{t\to\infty}\left(\frac{1}{(p-1)}-\frac{1}{(p-1)\cdot t^{p-1}}\right)\\ &=\frac{1}{p-1} \end{align*}\]

La serie converge.

Note

Para \(p=1\) es también aplicable la prueba de la integral y se tiene que

\[ \int_1^\infty \frac{dx}{x}=\lim_{t\to\infty}(\ln t -\ln 1)=\infty \]

es decir, la serie diverge.

Serie de potencias#

Tienen la forma

\[ \sum_{n=0}^\infty c_nx^n=c_0+c_1x+c_2x^2+\cdots \]

donde \(c_n\) son los coeficientes de la serie.

Son útiles para aproximar funciones y obtener integrales de la misma de manera más sencilla; para resolver ecuaciones diferenciales u obetener aproximaciones mediante polinomios.

En particular, las series de Taylor son series de potencias, que nos permiten aproximar una función \(f\) en el entorno de un punto \(a\): \((a-R,a+R)\).

Ejemplos#

  • El desarrollo de Taylor de orden \(n\) de la función \(e^x\) en \(a=0\) es:

\[ P_n(x)=1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\cdots+\frac{x^n}{n!} \]

Su resto está acotado por

\[ |R_n|\leq \frac{M}{(n+1)!}|x|^{n+1} \]

siendo \(M\) una cota a la derivada \(n+1\)-ésima de \(f\) (que es igual a \(e^x\)) en el intervalo \([0,x]\). Como la exponencial es creciente:

\[ |R_n|\leq \frac{e^x}{(n+1)!}x^{n+1},\qquad x\geq 0 \]

Como se cumple que \(\lim_{n\to\infty}R_n(x)=\), entonces \(\lim_{n\to\infty}T_n(x)=e^x\). Esto es, podemos aproximar \(e^x\) con su polinomio de Taylor, con la precisión que se necesite, sólo añadiendo términos a la serie.

\[ e^x=\sum_{n=0}^\infty\frac{x^n}{n!} \]

  • Función \(\ln(x)\) en \(a=1\)

El polinomio de Taylor es

\[ P_n(x)=\sum_{n=1}^\infty (-1)^{n-1}\frac{(x-1)^n}{n} \]

Como \(f^{(n+1}(x)=\frac{(-1)^n n!}{x^{n+1}}\) es decreciente en \([1,x]\), una cota en ese intervalo es \(M=1\).

El resto queda

\[ |R_n|\leq \frac{1}{n+1}|x-1|^{n+1} \]

No obstante, \(R_n\) sólo tiende a 0 (al hacer \(n\to\infty\)) si \(|x-1|<1\), por tanto el polinomio de Taylor no representa a \(\ln x\) si \(x>2\).

Ejercicio#

Obtener la suma de \(S=\sum_{i=1}^\infty\frac{5}{3^{n-1}}\)

Solución:

La serie es \(S=5+\frac{5}{3}+\frac{5}{3^2}+\frac{5}{3^3}+\cdots\). Es una serie geométrica de razón \(r=\frac{1}{3}\) con término inicial \(a=5\).

La suma es

\[ S=\frac{a}{1-r}=\frac{5}{1-\frac{1}{3}}=\frac{5}{\frac{2}{3}}=\frac{15}{2} \]