Problemas de optimización#
import sympy as sp
import matplotlib.pyplot as plt
x=sp.symbols('x')
def draw_rectangle(P1,P2,P3,P4,color='black',linestyle='-'):
p1, p2 = sp.Point(P1[0], P1[1]), sp.Point(P2[0], P2[1])
p3, p4 = sp.Point(P3[0], P3[1]), sp.Point(P4[0], P4[1])
plt.plot(*zip(p1,p2),color=color,linestyle=linestyle)
plt.plot(*zip(p2,p3),color=color,linestyle=linestyle)
plt.plot(*zip(p3,p4),color=color,linestyle=linestyle)
plt.plot(*zip(p4,p1),color=color,linestyle=linestyle)
#or alternatively
#plt.plot(*zip(p1, p2, p3, p4, p1))
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[1], line 1
----> 1 import sympy as sp
2 import matplotlib.pyplot as plt
3 x=sp.symbols('x')
ModuleNotFoundError: No module named 'sympy'
Problema 51#
Considere el siguiente problema: Se ha de construir una caja con la parte superior abierta, a partir de una pieza cuadrada de cartón de 3 dm de ancho, al recortar un cuadrado de cada una de las cuatro esquinas y doblar los lados hacia arriba. Encuentre el volumen más grande que puede tener una caja semejante.
P1=[0,0]
P2=[0,3]
P3=[3,3]
P4=[3,0]
draw_rectangle(P1,P2,P3,P4)
P1=[0,0]
P2=[0,1]
P3=[1,1]
P4=[1,0]
draw_rectangle(P1,P2,P3,P4,color='red',linestyle='--')
P1=[2,2]
P2=[3,2]
P3=[3,3]
P4=[2,3]
draw_rectangle(P1,P2,P3,P4,color='red',linestyle='--')
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[2], line 6
3 P3=[3,3]
4 P4=[3,0]
----> 6 draw_rectangle(P1,P2,P3,P4)
8 P1=[0,0]
9 P2=[0,1]
NameError: name 'draw_rectangle' is not defined
La función que queremos optimizar es \(V(x)=x\cdot (3-2x)^2\) y los valores que puede tomar la variable \(x\) (la decisión a tomar) son \(x\in [0,\frac{3}{2}]\).
Tenemos que encontrar el máximo absoluto de una función continua en un intervalo cerrado y acotado. Por el teorema de Weierstrass, sabemos que la función alcanza dicho máximo y estará, o bien en los puntos críticos, o en los extremos del intervalo.
Paso 1: hallar los puntos críticos. La función es un polinomio y está definida en \(\mathbb{R}\), por tanto los puntos críticos serán solamente los puntos donde la primera derivada se anule.
funcion = x*(3-2*x)**2
derivada = sp.diff(funcion,x)
ecuacion = sp.Eq(derivada,0)
puntosCriticos = sp.solveset(ecuacion,x)
puntosCriticos
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[3], line 1
----> 1 funcion = x*(3-2*x)**2
2 derivada = sp.diff(funcion,x)
3 ecuacion = sp.Eq(derivada,0)
NameError: name 'x' is not defined
Obtenemos dos puntos críticos, que, junto a los extremos del intervalo, forman nuestra lista de candidatos:
\(c_1=0\)
\(c_2=1/2\)
\(c_3=3/2\)
Ahora solamente debemos comparar el valor de la función en los candidatos \(c_i\), \(i=1,2,3\):
c1 = 0
c2 = sp.Rational(1/2)
c3 = 3/2
funcion.subs(x,c1),funcion.subs(x,c2),funcion.subs(x,c3)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[4], line 2
1 c1 = 0
----> 2 c2 = sp.Rational(1/2)
3 c3 = 3/2
4 funcion.subs(x,c1),funcion.subs(x,c2),funcion.subs(x,c3)
NameError: name 'sp' is not defined
Observamos que el máximo absoluto se obtiene en \(c_2=1/2\). El máximo absoluto de la función \(V(x)\) en \([0,3/2]\) se encuentra en dicho punto.
sp.plot(funcion,(x,0,3/2))
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[5], line 1
----> 1 sp.plot(funcion,(x,0,3/2))
NameError: name 'sp' is not defined
Es importante notar que, en la resolución de este ejercicio, no hemos usado la derivada segunda, ya que teníamos que buscar un extremo absoluto de una función continua en un intervalo cerrado y acotado.
Problema 52#
Un recipiente rectangular con la parte superior abierta ha de tener un volumen de 10 m3. La longitud de su base es el doble de su ancho. El material para la base cuesta 10€ por metro cuadrado; el de los costados, cuesta 6€ por metro cuadrado. Encuentre el costo de los materiales para tener el más barato de esos recipientes.
Solución: si \(x\) es el ancho de la base, entonces el largo es \(2x\) y la altura es \(h\). El volumen es \(V=10=2x^2h\).
h=sp.symbols('h')
ecuacionVolumen = sp.Eq(2*x**2*h,10)
ecuacionVolumen
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[6], line 1
----> 1 h=sp.symbols('h')
2 ecuacionVolumen = sp.Eq(2*x**2*h,10)
3 ecuacionVolumen
NameError: name 'sp' is not defined
El coste es igual al coste de los laterales más el coste de la base
Coste = 20*x**2+6*(2*x*h+2*2*x*h)
Coste
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[7], line 1
----> 1 Coste = 20*x**2+6*(2*x*h+2*2*x*h)
2 Coste
NameError: name 'x' is not defined
Tenemos una función de coste que depende de dos variables, \(x\) y \(h\). Podemos hallar una en función de otra a partir de la ecuación del volumen. Despejamos la \(h\) (el ejercicio es totalmente análogo si se despeja la \(x\)).
h_funcionde_x = sp.solveset(ecuacionVolumen,h)
h_funcionde_x
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[8], line 1
----> 1 h_funcionde_x = sp.solveset(ecuacionVolumen,h)
2 h_funcionde_x
NameError: name 'sp' is not defined
Usamos dicho valor en la función de coste:
h_funcionde_x_subs = list(h_funcionde_x)[0]
Coste_x = Coste.subs(h,h_funcionde_x_subs)
Coste_x
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[9], line 1
----> 1 h_funcionde_x_subs = list(h_funcionde_x)[0]
2 Coste_x = Coste.subs(h,h_funcionde_x_subs)
3 Coste_x
NameError: name 'h_funcionde_x' is not defined
Queda por ver qué valores de \(x\) son posibles. Es claro que no es posible usar el valor \(x=0\) (el volumen sería 0, cuando tiene que ser 10). Por tanto los valores posibles son \(x\in(0,\infty)\), que es un abierto no acotado.
No es posible aplicar el Teorema de Weierstrass para la búsqueda de máximos y mínimos.
Empezamos buscando los puntos críticos, que son donde
\(C'(x)=0\)
\(\nexists C'(x)\)
La función \(C'(x)\) es:
derivadaPrimera = sp.diff(Coste_x,x)
derivadaPrimera
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[10], line 1
----> 1 derivadaPrimera = sp.diff(Coste_x,x)
2 derivadaPrimera
NameError: name 'sp' is not defined
Es claro que no existe cuando \(x=0\), pero hemos excluído ese punto del intervalo de posibles decisiones.
Los puntos donde la derivada se anula son:
ecuacionPuntosCriticos = sp.Eq(derivadaPrimera,0)
sp.solveset(ecuacionPuntosCriticos,x)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[11], line 1
----> 1 ecuacionPuntosCriticos = sp.Eq(derivadaPrimera,0)
2 sp.solveset(ecuacionPuntosCriticos,x)
NameError: name 'sp' is not defined
Obtenemos tres puntos, de los cuales únicamente el primero es real. Pedimos a sympy que nos devuelva únicamente soluciones reales.
sp.solveset(ecuacionPuntosCriticos,x,sp.S.Reals)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[12], line 1
----> 1 sp.solveset(ecuacionPuntosCriticos,x,sp.S.Reals)
NameError: name 'sp' is not defined
puntoCritico = list(sp.solveset(ecuacionPuntosCriticos,x,sp.S.Reals))[0]
puntoCritico
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[13], line 1
----> 1 puntoCritico = list(sp.solveset(ecuacionPuntosCriticos,x,sp.S.Reals))[0]
2 puntoCritico
NameError: name 'sp' is not defined
Coste_x.subs(x,puntoCritico)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[14], line 1
----> 1 Coste_x.subs(x,puntoCritico)
NameError: name 'Coste_x' is not defined
En este momento sabemos que la función, en el punto \(P=(\frac{6^{\frac{2}{3}}}{2},90\sqrt[3]{6})\) tiene tangente horizontal (segmento rojo) en el punto crítico. Es posible que sea un máximo relativo (local) (morado), un mínimo relativo (amarillo) o un punto de silla (verde).
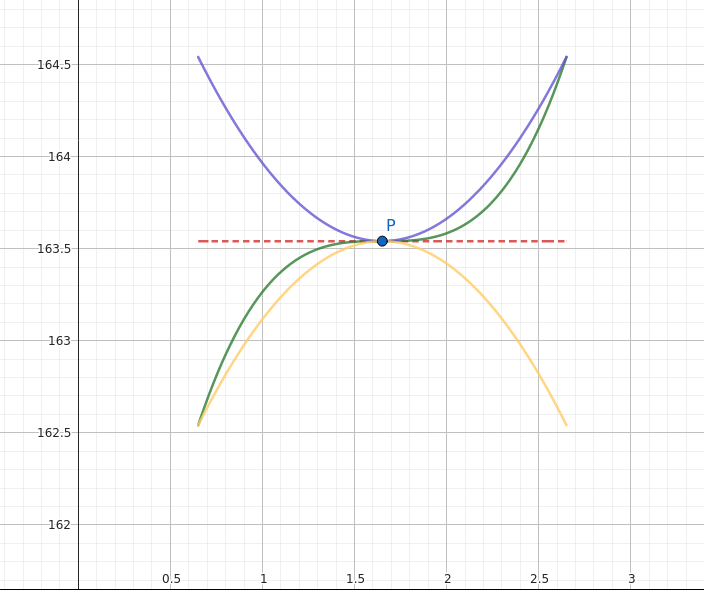
La derivada segunda evaluada en el punto \(x_{critico}= \frac{6^{\frac{2}{3}}}{2}\) nos sirve para averiguar en qué caso estamos.
derivadaSegunda = sp.diff(derivadaPrimera,x)
derivadaSegunda
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[15], line 1
----> 1 derivadaSegunda = sp.diff(derivadaPrimera,x)
2 derivadaSegunda
NameError: name 'sp' is not defined
derivadaSegunda.subs(x,puntoCritico)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[16], line 1
----> 1 derivadaSegunda.subs(x,puntoCritico)
NameError: name 'derivadaSegunda' is not defined
Obtenemos que \(C''(x_{critico})>0\), por tanto el punto crítico es un mínimo relativo (o local). No obstante, esto no nos asegura que éste es el punto que buscamos.
Para asegurarnos que el punto \(P\) es el punto buscado, es decir, el mínimo coste para cualquier valor de \(x\) (la decisión) posible debemos trabajar un poco más. Debemos asegurarnos que \(C(x_{critico})<C(x)\) para cualquier otro valor de \(x\) posible, que son los \(x>0\).
Vemos que \(C''(x)>0\) para \(x>0\). Entonces \(C'(x)\) es una función creciente. Como \(C'(x_{critico})=0\) entonces sucede que:
Si \(x\in(0,x_{critico})\) entonces \(C'(x)<0\), por lo tanto \(C(x)\) decrece.
Si \(x\in(x_{critico},\infty)\) entonces \(C'(x)>0\), por lo tanto \(C(x)\) crece.
De este modo queda probado que el valor de \(C(x)\) en el punto \(x_{critico}\) es el menor de todos los valores que toma la función cuando \(x>0\).
