Funciones racionales#
Una función racional es una función que es cociente de polinomios. Si
con \(a_n,b_m\neq 0\),la función:
es una función racional. El dominio de \(R(x)\) son todos aquellos puntos en \(\mathbb R\) donde no se anula el denominador \(Q(x)\) es decir, \(\mathbb R\setminus\{x:Q(x)=0\}\).
Ejemplos#
\(f(x)=\dfrac{x^3-2x}{2(x^2-5)}\) es una funci’on racional definida en \(\mathbb R\setminus\{{\pm\sqrt{5}}\}\).
\(g(x)=\dfrac{x^2+2}{x^2+1}\) es una funci’on racional definida en \(\mathbb R\).
\(M(x)=\dfrac{ax+b}{cx+d}\) con \(c\neq 0\) y \(ad-cb\neq 0\),
son transformaciones racionales lineales, y se llaman transformaciones de M”obius. Están definidas en \(\mathbb R\setminus\{-d/c\}\).
Descomposición en fracciones simples#
Una función racional (cuyo denominador es de grado mayor que el numerador) se descompone en fracciones simples cuando se escribe como suma de funciones racionales tales que en cada una de ellas su denominador solo tiene una raíz real o un par de complejos conjugados.
Ejemplos#
\(\dfrac{5x^2+20x+6}{x^3+2x^2+x}=\dfrac{6}{x}-\dfrac{1}{x+1}+\dfrac{9}{(x+1)^2}\).
\(\dfrac{2x^3-4x-8}{(x^2-x)(x^2+4)}=\dfrac{2}{x}-\dfrac{2}{x-1}+\dfrac{2x+4}{x^2+4}\).
Warning
La descomposición en fracciones simples es muy útil en integración.
Gráfica de una función racional#
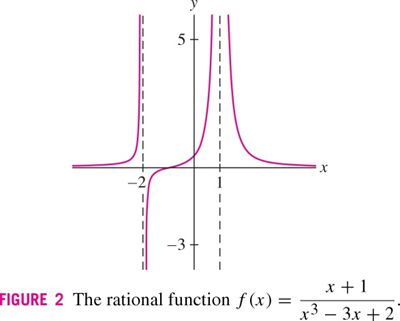
Fig. 18 Rogawski Calculus, Second Edition Copyright © 2012 W. H. Freeman and Company#
