Parametrizar la gráfica de \(f(x)\)#
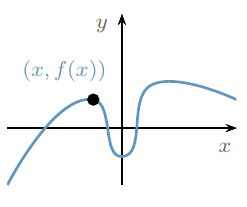
La gráfica de una función \(f:\mathbb{R}\rightarrow\mathbb{R}\) es una curva en el plano \(\mathbb{R}^2\)
\[
\mathcal{C}=\{(x,y):y=f(x),x\in\mathbb{R}\}
\]
Cuando \(x\) recorre \(\mathbb{R}\), el punto \((x,f(x))\) de \(\mathbb{R}^2\) varía proporcionando \(\mathcal{C}\).
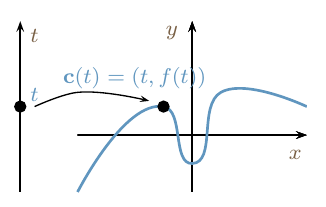
Podemos parametrizar \(\mathcal{C}\) fácilmente haciendo
\[
\mathbf{c}(t)=(t,f(t)),\quad t \in\mathbb{R}
\]
Cuando \(t\) recorre \(\mathbb{R}\), el punto \((t,f(t))\) varía proporcionando \(\mathcal{C}\).
Ejemplo#
La gráfica de la función \(f(x)=\frac{x^2}{4}+2x+7\) es la curva \(\mathcal{C}\)

Ecuación implícita de \(\mathcal{C}\):
\[
y=\frac{x^2}{4}+2x+7
\]
Parametrización de \(\mathcal{C}\):
\[
\mathbf{c}(s)=\left(s,\frac{s^2}{4}+2s+7\right)
\]
Otra posible parametrización:
\[
\mathbf{c}_2(t)=(2t-4,3+t^2)
\]
Ejercicio#
Hallar una ecuación implícita de las siguientes curvas
\[ x=t^2,\quad y=t^3,\quad 1\leq t\leq 2 \]\[ x=e^t,\quad y =\ln t\quad t>0 \]Razonar si las ecuaciones paramétricas e implícitas definen la misma curva
\[ x^2-y^2=1\qquad x=\cosh t,\quad y=\sinh t \]\[xy=1\qquad x=\cos t, \quad y=\sec t \]