Recta tangente. Aproximación lineal

Recta tangente

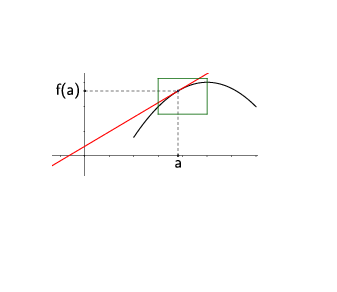
Si \(f\) tiene derivada en \(a\), la recta tangente a \(f\) en \(a\):

• pasa por \((a,f(a))\)

• tiene pendiente \(f'(a)\)

Note

La ecuación de la recta tangente a la gráfica de \(f\) en \(x=a\) es

\[ y=f(a)+f'(a)(x-a) \]

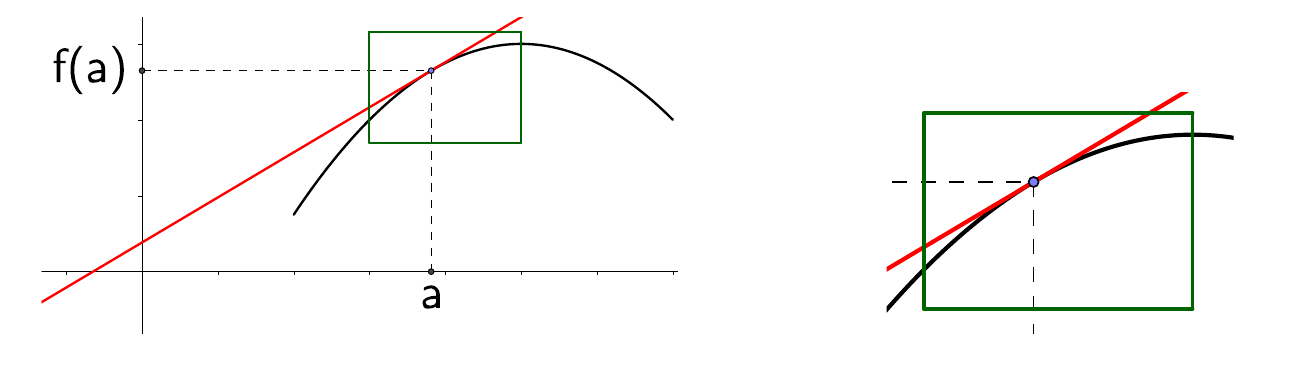
es la recta que pasa por el punto \((a,f(a))\) y tiene pendiente \(f'(a)\). De todas las rectas que pasan por ese punto, es la que más se aproxima a la función. A la recta tangente la llamamos la aproximación lineal de \(f\) en \(a\).

• Lineal porque es una recta

• Aproximación, porque se parece mucho a \(f\) cerca de \(a\)

Aproximaciones lineales

Queremos aproximar una función con la derivada primera.

Conocemos

• \(a\): el punto donde queremos aproximar la función

• \(f(a)\): el valor de la función en el punto

• \(f'(a)\): la pendiente de la recta tangente en ese punto

Queremos aproximar \(f(x)\) en valores de \(x\) cercanos a \(a\). Usaremos la recta tangente: \(y=f(a)+f'(a)(x-a)\)

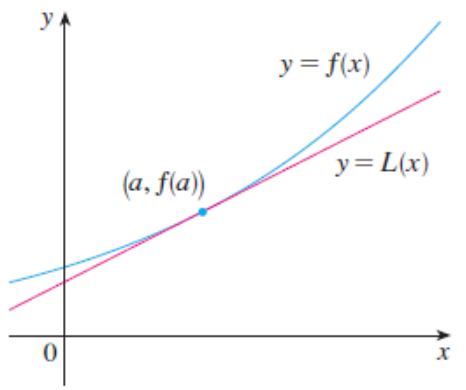
En ocasiones podemos usar la ecuación de la recta tangente a \(f\) en \(a\) en lugar de usar \(f\), para calcular \(f(x)\) en un punto \(x\) cerca de \(a\):

\[ f(x)\thickapprox f(a)+f'(a)(x-a),\quad \text{ si $x$ está cerca de $a$}. \]

• Esto permite sustituir una fórmula complicada (la de \(f\)) por algo más simple (la de la aproximación lineal)

• El precio a pagar es que hay un error

\[ error = f(x)-(f(a)+f'(a)(x-a)) \]

Ejemplo

Calcular \(\sqrt{3.9}\) mediante una aproximación lineal

Solución: consideramos \(f(x)=\sqrt{x}\). Como 3.9 está cerca de \(a=4\), y sabemos calcular \((4)=\sqrt{4}=2\), utilizamos la aproximación lineal de \(f\) con \(x=3.9\) y \(a=4\).

\[ f(x)\thickapprox f(a)+f'(a)(x-a)\Rightarrow f(3.9)=f(4)+f'(4)(3.9-4) \]

Como \(f'(x)=\frac{1}{2\sqrt{x}}\), entonces \(f'(4)=\frac{1}{4}\), por tanto:

\[ \sqrt{3.9}=f(3.9)\thickapprox 2+\frac{1}{4}(-0.1)=2-0.025 = 1.975 \]

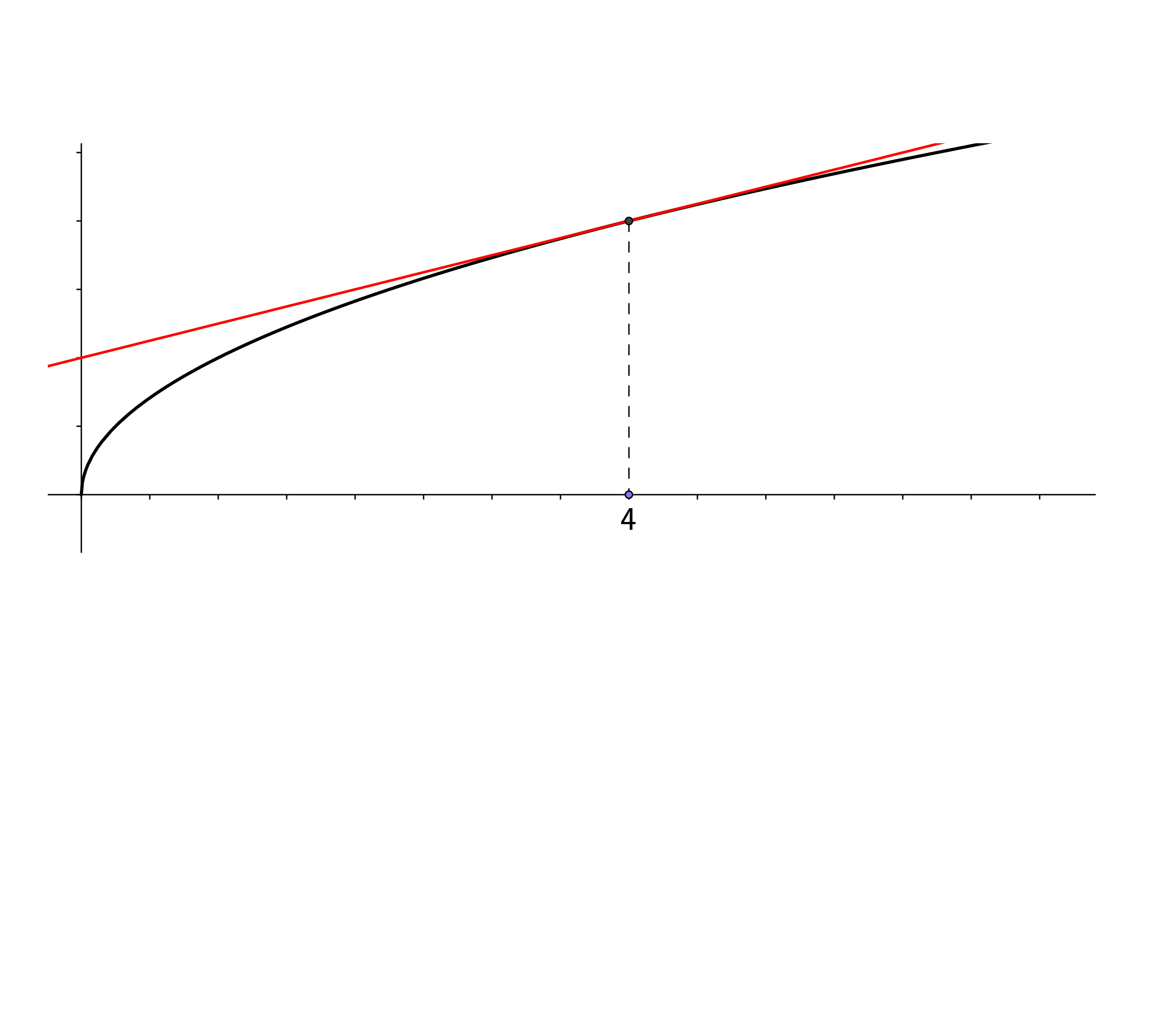
Se obtiene que el valor aproximado, 1.975, es mayor que el exacto \(\sqrt{3.9}\) (la gráfica de la recta tangente va por encima de la función).

Ejercicios

Aproximar linealmente los siguientes valores

• \(\sqrt{4.2}\)

• \(\sqrt[3]{(8.06)^2}\)

• \(e^{-0.015}\)

Tamaño del error

Si \(f\) tiene derivada, entonces

\[ f(x)={\color{blue}f(a)+f'(a)(x-a)}+\text{error}(x) \]

Warning

El error depende de \(x\) y se hace mayor a medida que \(x\) se aleja de \(a\)

¿Qué tamaño relativo tiene el error comparado con la distancia de \(f\) a \(a\)?

Despejando el error

\[ \text{error}(x)=f(x)-f(a)-f'(a)(x-a) \]

comparándolo con la distancia del punto \(x\) a \(a\)

\[ \frac{\text{error}(x)}{x-a}=\frac{f(x)-f(a)-f'(a)(x-a)}{x-a}=\frac{f(x)-f(a)}{x-a}-f'(a) \]

Tomando límites y usando la definición de derivada

\[ \lim_{x\to a}\frac{\text{error}(x)}{x-a}=\lim_{x\to a}\frac{f(x)-f(a)}{x-a}-f'(a)=0 \]

Usaremos la notación error\((x) = \mathcal{o}(x-a)\) cuando \(x \to a\). En otras palabras: es pequeño cuando se compara con \(x-a\) si \(x\) está cerca de \(a\).

Theorem 1

Si \(f\) es derivable en \(a\) entonces

\[ f(x)=f(a)+f'(a)(x-a)+\mathcal{o}(x-a).\qquad x\to a \]

Aplicación

Si \(f\) tiene derivada en \(x=a\) y \(f(a)+f'(a)(x-a)\neq 0\) es su aproximación lineal, entonces

\[ \lim_{x\to a}\frac{f(x)}{f(a)+f'(a)(x-a)}=1 \]

Motivo Usando que \(f(x)=f(a)+f'(a)(x-a)+\mathcal{o}(x-a)\) y aplicando las propiedades de los límites

\[\begin{align*} \lim_{x\to a}\frac{f(x)}{f(a)+f'(a)(x-a)}&= \lim_{x\to a}\frac{f(a)+f'(a)(x-a)+\mathcal{o}(x-a)}{f(a)+f'(a)(x-a)}\\ &= \lim_{x\to a}\frac{f(a)+f'(a)(x-a)}{f(a)+f'(a)(x-a)}+ \lim_{x\to a}\frac{\mathcal{o}(x-a)}{f(a)+f'(a)(x-a)} \\&= 1+0=1 \end{align*}\]

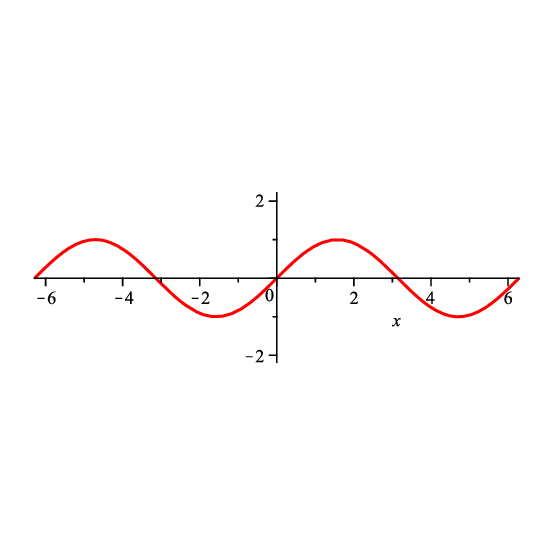
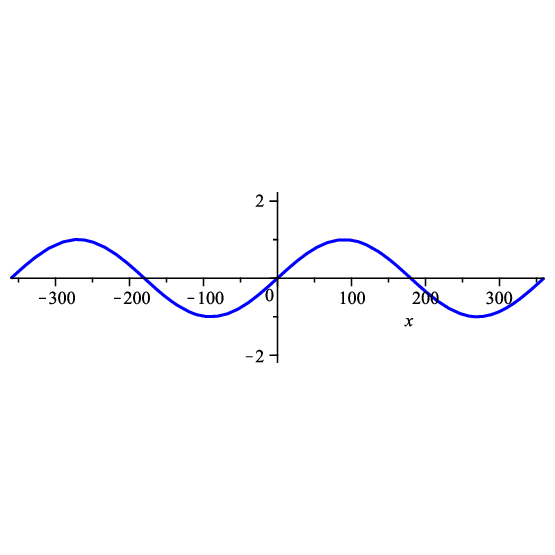
Aproximación lineal del seno en \(x=0\)

La recta tangente a \(f(x)=\sin x\) en \(x=0\) es \(y=x\)

Consecuencia:

\[ \lim_{x\to 0}\frac{\sin x}{x}=1 \]

Esto implica:

Note

La aproximación lineal de \(\sin x\) en \(x=0\) es

\[ \sin x = x + \mathcal{o}(x),\quad x\to 0 \]

Warning

Esta aproximación sólo es cierta si \(x\) está en radianes.

Si \(x=\frac{\pi}{36}\) rad = 5º (ángulo pequeño), entonces

\[ \sin\frac{\pi}{36}=0.08716\sim 0.08727 =\dfrac{\pi}{36}, \quad \textnormal{sin embargo,}\quad \sin 5^{\textnormal{o}} \nsim 5. \]

Aplicación

Ecuación de movimiento del péndulo simple

De la segunda ley de Newton y de la aceleración del movimiento circular se deduce la ecuación del movimiento del péndulo simple

\[ \frac{d^2\theta}{dt^2}=-\frac{g}{l}\sin\theta, \]

donde \(l\) es la longitud de la cuerca y \(g\) la aceleración de la gravedad.

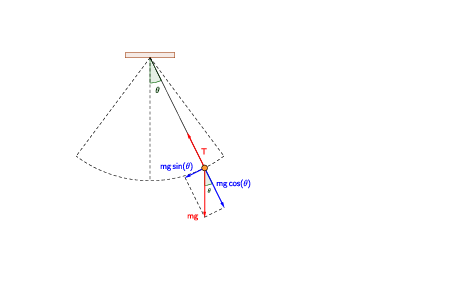
Cuando \(\theta\) pequeño (\(\theta\sim 0\)), se sustituye el seno por su aproximación lineal, \(\sin\theta\sim\theta\) y se obtiene,

\[ \dfrac{d^2\theta}{dt^2}=-\dfrac{g}{l}\theta \]

la ecuación del movimiento armónico simple.

Aproximación lineal de la exponencial en \(x=0\)

La recta tangente a \(f(x)=e^x\) en \(x=0\) es \(y=1+x\), por tanto:

Note

La aproximación lineal de \(e^x\) en \(x=0\) es

\[ e^x=1+x+\mathcal{o}(x),\quad x\to 0 \]

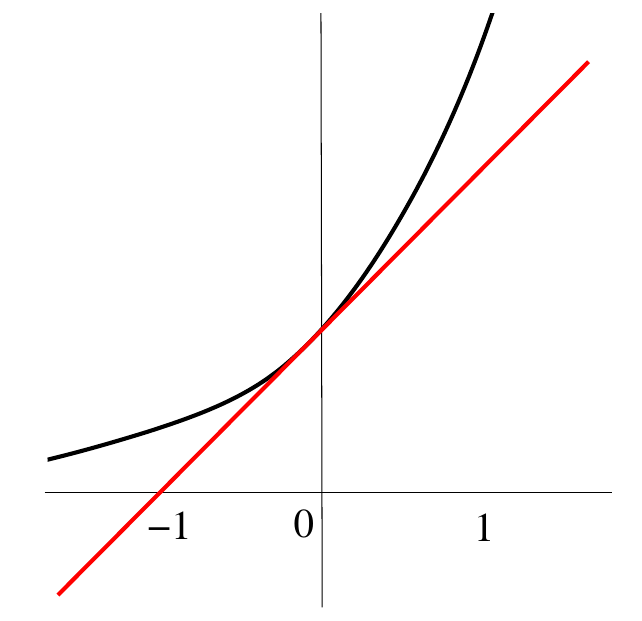
Fig. 30 \(f(x)=e^x\) en negro, \(y=x+1\) en rojo

• La función \(\log x\) es la inversa a \(e^x\), por tanto sus gráficas son simétricas respecto a \(y=x\)

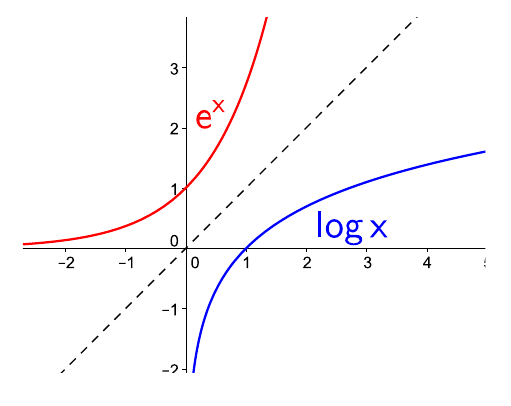
• la recta tangente a \(e^x\) en \(x=0\) pasa por el punto \((0,1)\) y será simétrica a la recta tangente a \(\log x\) en \(x=1\)

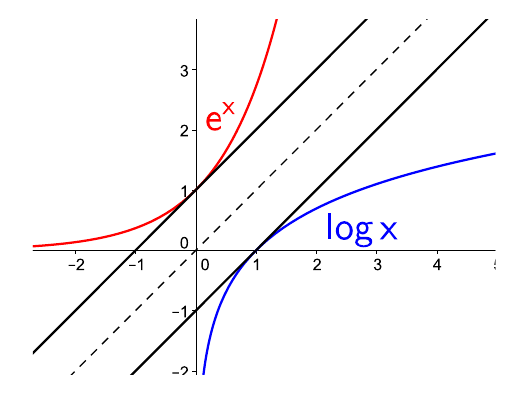
La recta \(y=x-1\) es la recta tangente a \(\log x\) en \(x=1\)

Note

la aproximación lineal de \(\log x\) en \(x=1\) es

\[ \log x = x-1 +\mathcal{o}(x-1),\quad x\to 1 \]

Aproximación lineal de la exponencial en \(x=0\)

La función \(g(x)=\log(1+x)\) está desplazada una unidad a la izquierda con respecto a \(\log x\), por tanto su recta tangente también está desplazada una unidad hacia la izquierda.

Note

Aproximación lineal de \(\log(1+x)\) en \(x=0\)

\[ \log(1+x)=x+\mathcal{o}(x),\quad x\to 0 \]

Diferenciales

Dada \(y=f(x)\), se define la diferencial de \(y\) como \(dy = f'(x)dx\). Podemos poner \(\Delta y = f'(x)\Delta x\), donde, de la recta tangente

\[ \Delta y = y-f(a),\qquad \Delta x = x-a \]