Optimización

Ejemplo: un agricultor tiene 2400 cm de material para construir una valla y desea cercar un campo rectangular a la orilla de un río recto. ¿Cuál es el campo del área máxima que puede cercar?

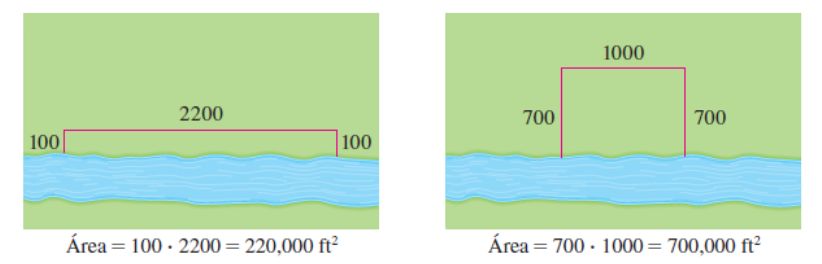
La función que define el área es \(A(x,y)=xy\). Tenemos la restricción \(2x+y=2400\) de donde despejamos una variable, por ejemplo, \(y=2400-2x\). Sustituyendo esta variable en la función obtenemos \(A(x)=x(2400-2x)=2400x-2x^2\), que es una función cuadrática con término principal negativo, por tanto sólo tiene un máximo absoluto y será en el punto donde \(A'(x)=0\). Sólo queda ver si es un valor posible.

Calculamos la derivada \(A'(x)=2400-4x\). Igualando a 0 obtenemos \(x=600\). El valor de \(y=2400-1200=1200\).

Los posibles valores de \(x\) son el intervalo \([0,1200]\). El punto crítico está en el interior del intervalo. En los extremos del intervalo el área vale 0, por tanto el máximo absoluto estará en \(x=600\).

Problema

Se ha de construir una caja con la parte superior abierta, a partir de una pieza cuadrada de cartón de 3 pies de ancho, al recortar un cuadrado de cada una de las cuatro esquinas y doblar los lados hacia arriba. Encuentre el volumen más grande que puede tener una caja semejante.

Problemas

• [Nov2018] Los barriles que se utilizan para almacernar petróleo tienen forma cilíndrica y capacidad de 160 litros. Hallar las dimensiones del cilindro para que la chapa empleada en la construcción sea mínima.

Solución:

El volumen de un cilindro es \(V=\pi\cdot r^2\cdot h\), donde \(r\) es el radio de la base y \(h\) la altura. Sabemos que \(V=160\), por tanto podemos despejar una de las dos variables:

\[ h=\frac{160}{\pi r^2} \]

El área total de un cilindro es el área de las tapas y el área lateral. El área de cada tapa es \(A_{tapa}=\pi r^2\). Por otra parte \(A_{lateral}=2\pi rh\). Por lo tanto

\[ A_{total}=2A_{tapa}+A_{lateral}=2\pi r^2+2\pi rh=2\pi r(r+h) =2\pi r(r+\frac{160}{\pi r^2}=2\pi r^2+\frac{320}{ r} \]

Derivando e igualando a cero

\[ A'(r)=2\pi r+\frac{320}{r}=0\Leftrightarrow r=\sqrt[3]{\frac{80}{\pi}} \]

La altura queda

\[ h=\frac{160}{\pi r^2}=\frac{160}{\pi \sqrt[3]{\frac{80}{\pi}}} =\frac{160}{\pi\left(\frac{80}{\pi}\right)^{\frac{2}{3}}}=\frac{100}{\sqrt{100\pi}} \]

$$

• [Julio2018] Se quiere obtener la tarjeta rectangular mayor posible aprovechando una cartulina triangular que tiene dos lados en ángulo recto de 20 y 30 cms. ¿Cuál será el tamaño mayor que se puede conseguir? Aplicar los resultados teóricos que aseguran que su área es máxima.

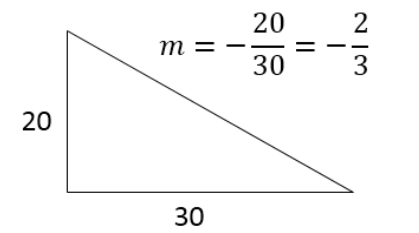
Recta de pendiente \(m=-2/3\) y que pasa por el punto \((30,0)\) es \(y=-\frac{2}{3}x+20\).

El área queda \(A=xy=-\frac{2}{3}x^2+20x\). Puntos sigulares \(A'(x)=-\frac{4}{3}x+20=0\). Entonces \(x=15\) e \(y=10\). El área es \(A=150\).

Ejercicio

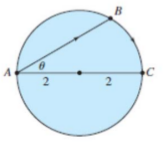
Una mujer que se encuentra en un punto \(A\) sobre la playa de un lago circular con radio de 2 kilómetros desea llegar al punto \(C\), opuesto al \(A\) sobre el otro lado del lago en el tiempo más corto posible. Puede caminar a razón de 4 km/h y remar en un bote a 2 km/h. ¿En qué ángulo en relación con el diámetro debe remar?