Interpretación#

Una curva se puede parametrizar de infinitas formas distintas.

Una parametrización de la curva describe la manera en la que se recorre dicha curva.

Se puede entender la curva como una carretera y una parametrización de la misma como un ciclista que la recorre.

Si el parámetro \(t\) representa el tiempo, \(c(t)\) representa la posición de una partı́cula en el instante \(t\).

\[\begin{align*} \mathbf{c}:[a,b]\longrightarrow \mathbb{R}^n \\ t\longmapsto \mathbf{c}(t) \end{align*}\]
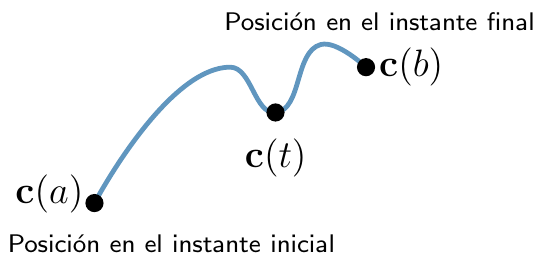
fishy

Curvas parametrizadas#

Una curva \(C\) en \(\mathbb{R}^n\) es un conjunto de puntos de Rn que puede describirse mediante un único parámetro que varı́a.

Consideremos una función vectorial \(\mathbf{c} : [a, b] \rightarrow \mathbb{R}^n\) con

\[ \mathbf{c}(t) = (x_1 (t), x_2 (t), . . . , x_n (t)) \]

  • La gráfica de \(c\) se dice que es una curva parametrizada \(C\) en \(\mathbb{R}^n\).

  • Se dice que la función vectorial \(c\) es una parametrización de la curva \(C\).

  • Los puntos \(c(a)\) y \(c(b)\) se llaman punto inicial y punto final respectivamente de la parametrización \(c\)

Note

En \mathbb{R}^2 se suele escribir \(\mathbf{c}(t)=(x(t),y(t))\)

Ejemplos#

  • Circunferencia

Implícitas: \(x^2+y^2=1\)

fishy

Parametrización

\[ x(t)=\cos t,\quad y(t)=\sin t\qquad t\in[0,2\pi) \]

  • Parábola

Implícitas: \(y=x^2\)

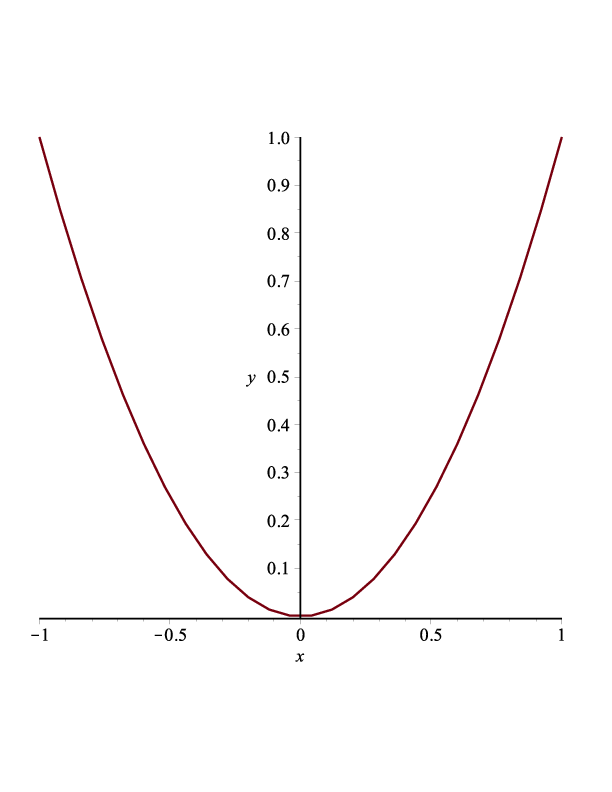
fishy

Parametrización:

\[ x(t)=t,\quad y(t)=t^2,\qquad t\in \mathbb{R} \]

Note

Si la curva parametrizada es la gráfica de una función, ésta puede encontrarse eliminando el parámetro