Funciones trigonométricas#
Warning
Los ángulos deben estar en radianes
Derivada del seno
\[
\frac{d}{dx}(\sin(x))=\cos(x)
\]
Demostración:
Necesitamos unos resultados previos
Teorema de la compresión#
\[
\lim_{x\to 0}\frac{\sin x}{x}=1
\]
Demostración:
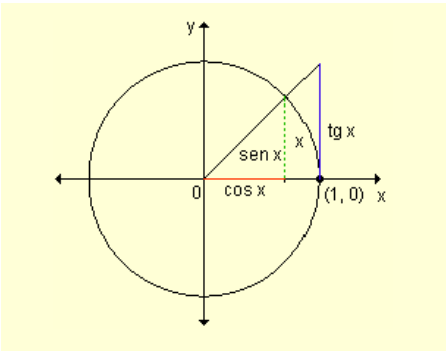
Tomamos ángulo \(x>0\) en radianes. La gráfica muestra como \(\sin x < x < \tan x\). Dividimos por \(\sin x (\neq 0)\):
\[
\frac{\sin x}{\sin x}<\frac{x}{\sin x}<\frac{\tan x}{\sin x}
\]
Simplificando
\[
1<\frac{x}{\sin x}<\frac{1}{\cos x}
\]
Invirtiendo (y usando la regla \(0\leq a<b\Rightarrow \frac{1}{b}<\frac{1}{a}\))
\[
\cos x<\frac{\sin x}{x}<1
\]
Tomando límites cuando \(x\to 0\)
Note
Recordatorio:
\[
\lim_{x\to 0}\cos x =1
\]
\[
\lim_{x\to 0}\cos x<\lim_{x\to 0}\frac{\sin x}{x}<\lim_{x \to 0}1
\]
usando el teorema de la compresión tenemos
\[
\lim_{x\to 0}\frac{\sin x}{x}=1
\]
Límite#
\[\begin{align*}
\lim_{h\to 0}\frac{\cos h-1}{h}&=\lim_{h\to 0}\frac{\cos h-1}{h}\frac{\cos h+1}{\cos h+1}\\
&=\lim_{h\to 0}\frac{\cos^2h-1}{h(\cos h+1)}\\
&=\lim_{h\to 0}\frac{-\sin^2 h}{h(\cos h+1)}\\
&-\lim_{h\to 0}\frac{\sin h}{h}\frac{\sin h}{(\cos h+1)}\\
&=-1\left(\frac{0}{1+1}\right)=0
\end{align*}\]
Seno#
Usaremos los resultados anteriores para hallar la derivada de \(f(x)=\sin(x)\)
\[\begin{align*}
f'(x)&=\lim_{h\to0}\frac{\sin(x+h)-\sin(x)}{h}\\
&=\lim_{h\to0}\frac{\sin x\cos h+\cos x\sin h-\sin x}{h}\\
&=\lim_{h\to0}\left(
\frac{\sin x\cosh-\sin x}{h}-\frac{\cos x\sin h}{h}\right)\\
&=\lim_{h\to0}\left(
\sin x\frac{\cos h -1}{h}+\cos x\frac{\sin h}{h}
\right)\\
&=\cos x
\end{align*}\]
Otras funciones#
\[
[\cos x]' = -\sin x
\]
\[
[\csc x]' = -\csc x\cot x
\]
\[
[\sec x]' = -\sec x\tan x
\]
\[
[\tan x]' = \sec^2 x = 1 + \tan^2 x
\]
\[
[\cot x]' = -\csc^2 = \cot^2-1
\]
